bărbați. Simt, cumva, că îmi place ceea ce spui.
Soc. Și mie, Meno, îmi place ce spun.
Din meno lui Platon
lungimea diagonalei pătratului unității este egală cu rădăcina pătrată a lui 2.
lungimea diagonalei pătratului unității este egală cu √2. Ei bine, acest lucru nu este într-adevăr o veste mare. Toți cei care au întâlnit teorema lui Pitagora sunt conștienți de acest fapt., În triunghiul drept izoscel cu picioarele de lungime 1, hypotenuse, conform teoremei pitagoreice – 12 + 12 = (hypotenuse)2 – este într-adevăr de lungime √2. Motivația pentru această pagină nu este atât de mult faptul în sine, ci modul de a o arăta fără a recurge la faimoasa teoremă. Într-adevăr, s-ar putea argumenta că teorema lui Pitagora ar fi putut fi suprautilizată, vezi un exemplu curios.un argument care se întoarce la figura desenată de Socrate în meno-ul lui Platon ar fi putut fi cunoscut chiar de Pitagora, deși acesta din urmă a trăit cu un secol mai devreme.,
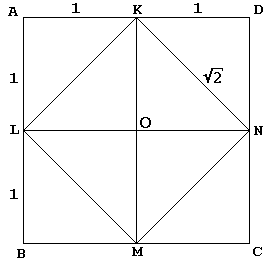
În caseta de dialog, Socrate, în maniera sa obișnuită, conduce un tânăr sclav la o constructie de un pătrat de două ori zona de date:
având în piața KLMN cu centrul O este mai întâi tăiat prin diagonale în 4 triunghiuri egale. Socrate încorporează KLMN într-un pătrat mai mare ABCD ca și cum ar reflecta aceste triunghiuri fiecare în ipotenuza sa. Sclavul recunoaște atunci – și cine nu ar face-o? – acel ABCD pătrat este de două ori mai mare decât KLMN pătrat.
adevărul este că ABCD-ul pătrat al lui Socrate a măsurat 4 pe lateral, astfel încât piața KLMN avea o suprafață de 8., Este clar că atunci când începem cu pătratul ABCD al laturii 2 (și, prin urmare, al zonei 4), piața KLMN va avea Suprafața 2.acum, în general, pentru un număr pozitiv A, √A este definit ca un număr al cărui pătrat este A:
(√a)2.pe de altă parte, fiecare student din zone știe, că zona unui pătrat din partea b este egală cu b2. Rezultă apoi că latura unui pătrat cu zona A este exact √A. concluzionăm că latura pătratului KLMN este egală cu √2. Pentru unul,
KN = √A.
punctul central al argumentului este faptul că, în diagramă, KN joacă un rol dublu., Pe lângă faptul că este una dintre laturile pătrat KLMN, de asemenea, servește ca o diagonală de pătrat OKDN. Acesta din urmă este, desigur, un pătrat de unitate, ceea ce dovedește afirmația noastră.
(dintr-o perspectivă puțin diferită, același episod este menționat în altă parte.)
















Lasă un răspuns