Figura Triunghi Unghi-Latura-Unghi (ASA)
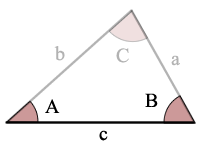
O = unghiul
B = unghiul B
C = unghiul C
o = parte a
b = latura b
c = partea c
P = perimetrul
s = semi-perimetrul
K = aria
r = raza cerc înscris
R = raza cerc circumscris
Calculator de Utilizare
Fiecare opțiune calcul, prezentat mai jos, are sub-gloanțe lista secvența de metode utilizate în acest calculator pentru a rezolva pentru unghi necunoscut și partea valori, inclusiv Suma Unghiurilor într-un Triunghi, Legea Sines și Legea de Ambianta., Acestea nu sunt singurele secvențe pe care le-ați putea folosi pentru a rezolva aceste tipuri de probleme.
- a se Vedea, de asemenea, aceste Trigonometrie Calculatoare:
- Legea de Ambianta Calculator
- Legea Sines Calculator
Rezolvarea Triunghiului Teoreme
AAA este Unghi, Unghi, Unghi
Specificarea cele trei unghiuri ale unui triunghi nu se identifica în mod unic un triunghi. Prin urmare, specificarea a două unghiuri ale unui tringle vă permite să calculați numai al treilea unghi., având în vedere dimensiunile a 2 unghiuri ale unui triunghi, puteți calcula dimensiunea celui de-al treilea unghi. Totalul va fi egal cu 180 ° sau π radiani.
C = 180° – A – B (în grade)
C = π – A – B (în radiani)
AAS este unghi, unghi, latură
având în vedere dimensiunea a 2 unghiuri și 1 latură opusă unuia dintre unghiurile date, puteți calcula dimensiunile unghiului 1 rămas și 2 laturi.
folosiți regula suma unghiurilor pentru a găsi celălalt unghi, apoi
utilizați Legea sinelor pentru a rezolva pentru fiecare dintre celelalte două părți.,
ASA este unghiul, latura, unghiul
având în vedere dimensiunea unghiurilor 2 și dimensiunea laturii care se află între acele unghiuri 2, puteți calcula dimensiunile unghiului 1 și laturilor 2 rămase.
folosiți regula suma unghiurilor pentru a găsi celălalt unghi, apoi
utilizați Legea sinelor pentru a rezolva pentru fiecare dintre celelalte două părți.,
ASS (sau SSA) este unghi, lateral, lateral
având în vedere dimensiunea laturilor 2 (a și c unde a < c) și dimensiunea unghiului A care nu se află între cele 2 laturi, este posibil să puteți calcula dimensiunile laturilor 1 și 2 rămase, în funcție de următoarele condiții.,f Ambianta pentru a rezolva pentru fiecare dintre celelalte două unghiuri
prezent 2 solutii complete
Exemplu: 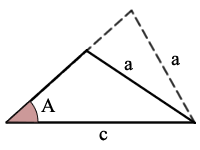
sin(A) = a/c, există un posibil triunghi
folositi Legea Sinusurilor pentru a rezolva pentru un unghi, C
utilizarea Suma de Unghiuri Regulă pentru a găsi alt unghi, B
folositi Legea Sinusurilor pentru a rezolva pentru ultima parte, b
Exemplu: 
sin(A) > un/c, nu există triunghiuri
Notificare de Eroare: sin(O) > o/c astfel încât nu există nici soluții și nici triunghi!,
Exemplu: 
SAS este Parte, Unghi, Lateral
Având în vedere dimensiunea de 2 părți (c și o) și mărimea unghiului B, care este în între cele 2 părți se pot calcula dimensiunile rămase partea 1 și 2 unghiuri. utilizați Legea Cosinusurilor pentru a rezolva pentru partea rămasă, b
determinați care parte, a sau c, este cea mai mică și folosiți Legea sinelor pentru a rezolva pentru dimensiunea unghiului opus, respectiv A sau C.,
folosiți regula suma unghiurilor pentru a găsi ultimul unghi
SSS este lateral, lateral, lateral
având în vedere dimensiunile celor 3 laturi, puteți calcula dimensiunile tuturor celor 3 unghiuri din Triunghi. utilizați Legea cosinus pentru a rezolva unghiurile. Puteți utiliza, de asemenea, regula suma unghiurilor pentru a găsi unghiul final odată ce cunoașteți 2 dintre ele.,sin-1
Legea de Ambianta
Dacă a, b și c sunt lungimile de picioare de un triunghi opuse unghiurilor a, B și C respectiv; atunci legea de ambianta membre:
a2 = c2 + b2 – 2bc cos A, rezolvarea pentru cos A, cos a = ( b2 + c2 – a2 ) / 2bc
b2 = a2 + c2 – 2ca cos B, rezolvarea pentru cos B, cos B = ( c2 + a2 – b2 ) / 2ca
c2 = b2 + a2 – 2ab cos C, rezolvarea pentru cos C cos C = ( a2 + b2 – c2 ) / 2ab
Rezolvarea problemelor, de exemplu, pentru un unghi, O = cos-1
Alte Triunghi Caracteristici
Triunghiul perimetrul P = a + b + c
Triunghi semi-perimetrul, s = 0.,5 * (a + b + c)
zona Triunghiul, K = √
Raza de cerc înscris în triunghi, r = √
Raza cerc circumscris în jurul triunghiului, R = (abc) / (4K)
Referințe/ bibliografie
Weisstein, Eric W. „FUNDUL Teorema.”De La MathWorld – O Resursă Web Wolfram. Teorema fundului.
matematica este distractiv-rezolvarea triunghiuri SAS
















Lasă un răspuns