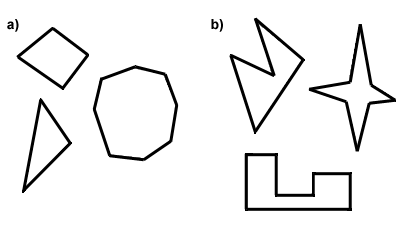
poligoane convexe și Concave
fiecare poligon este convex sau concav. Diferența dintre poligoanele convexe și concave constă în măsurile unghiurilor lor. Pentru ca un poligon să fieconvexe, toate unghiurile sale interioare trebuie să fie mai mici de 180 de grade. În caz contrar, poligonul esteconcavă. Un alt mod de a gândi este acesta: diagonalele unui convexpolygon vor fi toate în interiorul poligonului, în timp ce anumite diagonale ale unui poligon concav se vor afla în afara poligonului, pe exteriorul său., Below in Part A are some convex polygons, and in Part B, some concave polygons. In the rest of this text, you can assume that every polygon discussed is convex.
Regular Polygons
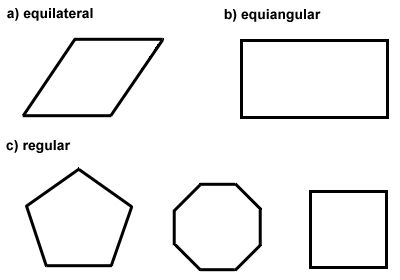
Polygons can also be classified as equilateral, equiangular, or both. Equilateral polygons have congruent sides, like a rhombus. Equiangular polygons have congruent interior angles, like a rectangle., Atunci când un poligon este atât echilateral și equiangular, este numit un poligon regulat. Un pătrat este un exemplu de poligon regulat. Centrul unui poligon regulat este punctul din care toate vârfurile poligonului sunt echidistante. Poligoanele obișnuite au proprietăți speciale pe care le vom explora în secțiunea următoare. Mai jos sunt câteva exemple de poligoane equiangulare, echilaterale și regulate.,
Congruent Polygons
One more note on polygons: Polygons whose sides are all congruent are congruent polygons. Knowing this term will be important later. In congruent polygons, every segment is congruent.
















Lasă un răspuns