Când unghiurile unui triunghi nu se adaugă până la 180 de grade

1. Nu unghiurile unui triunghi adăuga până la 180 de grade sau$ \ pi $ radiani? Răspunsul este „uneori Da, Uneori nu”. Este aceasta o întrebare importantă? Da, pentru că duce la înțelegerea faptului că există geometrii diferite bazate pe axiome diferite sau „reguli ale jocului geometriei”. Este o întrebare semnificativă? Ei bine, nu, cel puțin nu până când nu am convenit asupra sensului cuvintelor „unghi” și „triunghi”, nu până când nu cunoaștem regulile jocului., În acest articol vom discuta pe scurt axiomele care stau la baza și să dea o dovadă simplă că suma unghiurilor unui triunghi pe suprafața unei sfere unitate nu este egal cu $\pi$, dar la $\pi$ plus aria triunghiului. Vom folosi faptul că suprafața suprafeței unei sfere unitate este $ 4 \ pi$.

2. Teorema mare

înainte de a putea spune ce este un triunghi, trebuie să fim de acord asupra a ceea ce înțelegem prin puncte și linii. Lucrăm la geometria sferică (literalmente geometrie pe suprafața unei sfere)., În această geometrie spațiul este suprafața sferei; punctele sunt puncte de pe acea suprafață, iar linia cea mai scurtă distanță dintre două puncte este marele cerc care conține cele două puncte. Un cerc mare (cum ar Ficuatorul) taie sfera în două emisfere egale. Această geometrie are aplicații evidente la distanțele dintre locuri și rutele aeriene de pe Pământ.,unghiul dintre două cercuri mari într-un punct P este unghiul euclidian între direcțiile cercurilor (sau strict între tangentele cercurilor la P). Acest lucru nu prezintă dificultăți în navigarea pe Pământ, deoarece în orice moment dat ne gândim la unghiul dintre două direcții ca și cum Pământul ar fi plat în acel moment.o lună este o parte a suprafeței sferei delimitată de două cercuri mari care se întâlnesc în puncte antipodale., Mai întâi luăm în considerare zona unei lune și apoi introducem un alt cerc mare care împarte luna în triunghiuri.

sferă rotativă care arată 4 lunes

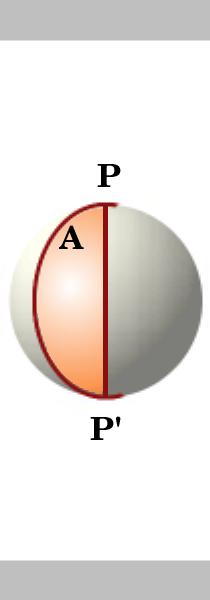
Lema.aria unei lune pe un cerc cu raza unității este de două ori unghiul său, adică dacă unghiul lunei este A, atunci suprafața sa este 2a. două cercuri mari care se intersectează la punctele antipodale P și P’ împart sfera în 4 lunes. Suprafața suprafeței unei sfere de unitate este de $4 \ pi$.,

zonele de lunes sunt proporționale cu unghiurile lor de la P astfel încât zona de o lune cu unghiul a este

${\frac{A}{2\pi}\times {4\pi}= {2A}}$

Exercitiul 1.care sunt zonele celorlalte 3 lunes? Zonele 4 adăuga până la $4 \ pi$?

verificați răspunsurile aici .laturile unui triunghi ABC sunt segmente de trei cercuri mari care de fapt taie suprafața sferei în opt triunghiuri sferice. Între cele două cercuri mari prin punctul A există patru unghiuri., Am eticheta unghiul în interiorul triunghiului ABC cu unghiul A, și în mod similar celorlalte unghiuri ale triunghiului ABC cu unghiul B și unghiul C.

Rotative sfera arată 8 triunghiuri

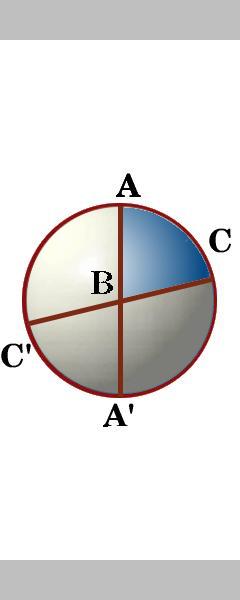
2

Rotirea sferei poți numi opt triunghiuri și spune dacă vreunul dintre ei avea aceeași zonă? Verificați răspunsurile aici .

Teorema.luați în considerare un triunghi sferic ABC pe sfera unității cu unghiurile A, B și C. Atunci aria triunghiului ABC este

A + B + C – $\pi$.,

diagrama arată o vedere privind în jos pe emisfera care are linia prin AC ca limita sa. Regiunile marcate Zona 1 și Zona 3 sunt lunes cu unghiuri A și C, respectiv. Luați în considerare lunes prin B și B’. Triunghiul ABC este congruent cu triunghiul A ‘B’ C’ astfel încât zona umbrită în formă de papion, zona marcată 2, Care este suma ariilor triunghiurilor ABC și A’bc’, este egală cu zona lunei cu unghiul B, adică egală cu 2b.,deci, în diagramă vedem zonele A trei lunes și, folosind lema, acestea sunt:

Zona 1 = 2a
Zona 2 = 2b
Zona 3 = 2C

în adăugarea acestor trei zone includem aria triunghiului ABC de trei ori., Hence

3., Geometria non-euclidiană

uneori descoperirile revoluționare nu sunt altceva decât să vedem de fapt ceea ce a fost sub nasul nostru tot timpul. Acesta a fost cazul descoperirii geometriei non-euclidiene în secolul al XIX-lea. Pentru unii 2000 de ani după Euclid scris „Elemente” în 325 Î. hr. oamenii au încercat să demonstreze postulatul ca o teoremă din geometrie din celelalte axiome, dar nu a reușit și e o poveste lungă., Între timp, matematicienii foloseau geometria sferică tot timpul, o geometrie care se supune celorlalte axiome ale geometriei euclidiene și conține multe dintre aceleași teoreme, dar în care postulatul paralel nu ține. De-a lungul timpului au avut un exemplu de geometrie non-euclidiană sub nasul lor.gândiți-vă la o linie L și un punct P nu pe L. marea întrebare este: „câte linii pot fi trase prin p paralel cu L?”În geometria euclidiană răspunsul este” exact unul ” și aceasta este o versiune a postulatului paralel., Dacă suma unghiurilor fiecărui triunghi din geometrie este $ \ pi $ radians, atunci postulatul paralel ține și invers, cele două proprietăți sunt echivalente.în geometria sferică, axiomele de bază pe care le presupunem (regulile jocului) sunt diferite de geometria euclidiană – aceasta este o geometrie non-euclidiană. Am văzut că în geometria sferică unghiurile triunghiurilor nu se adaugă întotdeauna la$ \ pi $ radiani, așa că nu ne-am aștepta ca postulatul paralel să țină., În geometria sferică, liniile drepte (linii de cea mai scurtă distanță sau geodezice)sunt cercuri mari și fiecare linie din geometrie taie fiecare altă linie în două puncte. Răspunsul la marea întrebare despre paralele este`dacă avem o linie L și un punct P nu pe L, atunci nu există linii prin p paralel cu linia L.,”

matematicieni greci (de exemplu Ptolemeu c 150) calculat măsurători de unghi drept triunghiuri sferice și a lucrat cu formule de trigonometrie sferică și matematicieni Arabi (de exemplu Jabir ibn Aflah c 1125 și Nasir ed-din c 1250) a extins și mai mult. Formula discutată în acest articol a fost descoperită de Harriot în 1603 și publicată de Girard în 1629. Alte idei ale subiectului au fost dezvoltate de Saccerhi (1667-1733).,toate acestea au fost în mare parte neobservate de descoperitorii secolului al XIX-lea ai geometriei hiperbolice, care este o altă Geometrie non-euclidiană în care postulatul paralel nu deține. În geometria sferică (numită și geometrie eliptică) unghiurile triunghiurilor adaugă până la mai mult de $\pi$ radiani, iar în geometria hiperbolică unghiurile triunghiurilor adaugă până la mai puțin de $\pi$ radiani.

pentru mai multe lecturi, vezi articolul lui Alan Beardon ” câte geometrii există?”și articolul lui Keith Carne „geometrii ciudate”., Există câteva activități practice pe care le puteți încerca pentru a explora aceste geometrii în continuare pentru a fi găsite la http://nrich.maths.org/MOTIVATE/conf8/index.html