afișare anunț mobil afișează toate notele ascunde toate notele
Secțiunea 3-1 : Ecuații Parametrice și Curbe
La acest moment (în ambele Calcule am și Calcul al II-lea) ne-am uitat aproape exclusiv la funcții în forma \(y = f\left( x \right)\) sau \(x = h\left( y \right)\) și aproape toate formulele care le-am dezvoltat cere ca funcțiile să fie într-una din aceste două forme. Problema este că nu toate curbele sau ecuațiile pe care am dori să le analizăm cad ușor în această formă.
luați, de exemplu, un cerc. Este destul de ușor să scrieți ecuația unui cerc centrat la origine cu raza \(r\).,cu toate acestea, nu vom putea niciodată să scriem ecuația unui cerc în jos ca o singură ecuație în oricare dintre formele de mai sus. Sigur că putem rezolva pentru \(x\) sau \(y\) ca următoarele două formule arată
\
dar există, de fapt, două funcții în fiecare dintre acestea. Fiecare formulă oferă o porțiune a cercului.din păcate, de obicei lucrăm la întregul cerc sau pur și simplu nu putem spune că vom lucra doar la o parte din acesta. Chiar dacă putem restrânge lucrurile la doar una dintre aceste porțiuni, funcția este încă adesea destul de neplăcută pentru a lucra.,
\
această a treia variabilă este de obicei notată cu \(t\) (așa cum am făcut aici), dar nu trebuie să fie desigur. Uneori vom restricționa valorile \(t\) pe care le vom folosi și alteori nu le vom folosi. acest lucru va depinde adesea de problemă și de ceea ce încercăm să facem.
pentru a ajuta la vizualizarea doar ceea ce o curbă parametrică este pretinde că avem un rezervor mare de apă, care este în mișcare constantă și am picătură o minge de ping-pong în rezervor., Punctul \(\left ({x, y} \ right) = \left( {F \left( t\right), g \left( t \right)}\ right)\) va reprezenta apoi locația mingii de ping pong în rezervor la momentul\ (t\), iar curba parametrică va fi o urmă a tuturor locațiilor mingii de ping pong. Rețineți că acest lucru nu este întotdeauna o analogie corectă, dar este util inițial pentru a ajuta la vizualizarea doar ceea ce este o curbă parametrică.schițarea unei curbe parametrice nu este întotdeauna un lucru ușor de făcut. Să aruncăm o privire la un exemplu pentru a vedea o modalitate de a schița o curbă parametrică., Acest exemplu va ilustra, de asemenea, de ce această metodă nu este de obicei cea mai bună.
în acest moment singura noastră opțiune pentru schițarea unei curbe parametrice este de a alege valorile \(t\), conectați-le în ecuațiile parametrice și apoi complot punctele. Deci, să conectăm unele \(t\).,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Din păcate, nu există un răspuns real la această întrebare în acest moment. Pur și simplu alegem \(t\) până când suntem destul de încrezători că avem o idee bună despre cum arată curba. Această problemă cu alegerea valorilor „bune” ale \(t\) face ca această metodă de schițare a curbelor parametrice să fie una dintre alegerile mai sărace. Uneori nu avem de ales, dar dacă avem de ales, ar trebui să o evităm.
vom discuta o metodă alternativă de grafică în exemplele ulterioare care vor ajuta la explicarea modului în care au fost alese aceste valori ale \(t\).,
Mai avem o idee de discutat înainte de a schița curba. Curbele parametrice au o direcție de mișcare. Direcția de mișcare este dată de creșterea \(t\). Deci, atunci când trasăm curbe parametrice, includem și săgeți care arată direcția mișcării. De multe ori vom da valoarea lui \(t\) care a dat puncte specifice pe grafic, de asemenea, pentru a clarifica valoarea lui \(t\) care a dat acel punct.
iată schița acestei curbe parametrice.
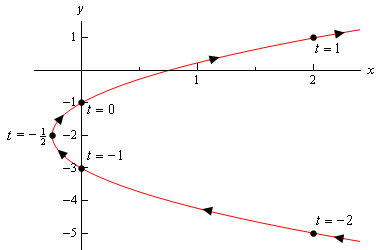
deci, se pare că avem o parabolă care se deschide spre dreapta.,înainte de a încheia acest exemplu, există un punct oarecum important și subtil pe care trebuie să-l discutăm mai întâi. Observați că ne – am asigurat să includem o porțiune a schiței din dreapta punctelor corespunzătoare \(t = – 2\) și \(t = 1\) pentru a indica faptul că există porțiuni ale schiței acolo. Dacă am fi oprit pur și simplu schița în acele puncte, indicăm că nu a existat nicio porțiune a curbei din dreapta acelor puncte și în mod clar va exista. Doar că nu am calculat niciunul dintre aceste puncte.,
Acest lucru poate părea un punct neimportant, dar după cum vom vedea în exemplul următor, este mai important decât am putea crede.
înainte de a aborda o modalitate mult mai ușoară de a schița acest grafic, să abordăm mai întâi problema limitelor parametrului. În exemplul anterior nu am avut limite asupra parametrului. Fără limite asupra parametrului, graficul va continua în ambele direcții, așa cum se arată în schița de mai sus.cu toate acestea, vom avea adesea limite asupra parametrului și acest lucru va afecta schița ecuațiilor parametrice., Pentru a vedea acest efect, să ne uităm la o ușoară variație a exemplului anterior.
rețineți că singura diferență aici este prezența limitelor pe \(t\). Toate aceste limite fac este să ne spună că nu putem lua orice valoare de \(t\) în afara acestui interval. Prin urmare, curba parametrică va fi doar o porțiune a curbei de mai sus. Iată curba parametrică pentru acest exemplu.,
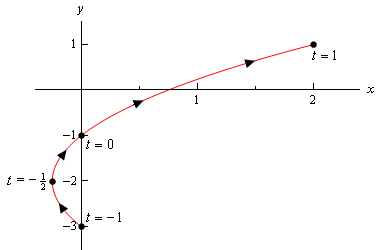
Observați că, cu această schiță pe care am pornit și oprit schita pe puncte originare din punctele de capăt ale gamei de \(t\)’s. Contrast cu schița în exemplul anterior, unde am avut o parte din schita a dreptul de „start” și „end” puncte pe care am calculat-o.
în acest caz, curba începe la \(t = – 1\) și se termină la \(t = 1\), în timp ce în exemplul anterior curba nu a început cu adevărat la cele mai multe puncte corecte pe care le-am calculat., Trebuie să fim clari în schițele noastre dacă curba începe / se termină chiar într-un punct sau dacă acel punct a fost pur și simplu primul/ultimul pe care l-am calculat.
acum este timpul să aruncăm o privire la o metodă mai ușoară de a schița această curbă parametrică. Această metodă folosește faptul că în multe, dar nu toate, cazuri putem elimina efectiv parametrul din ecuațiile parametrice și obținem o funcție care implică doar \(x\) și \(y\). Vom numi uneori această ecuație algebrică pentru a o diferenția de ecuațiile parametrice originale., Vor exista două mici probleme cu această metodă, dar va fi ușor să abordăm aceste probleme. Este important să rețineți totuși că nu vom fi întotdeauna capabili să facem acest lucru.
modul în care eliminăm parametrul va depinde de ecuațiile parametrice pe care le avem. Să vedem cum să eliminăm parametrul pentru setul de ecuații parametrice cu care am lucrat până în acest moment.
obținerea unei schițe a curbei parametrice odată ce am eliminat parametrul pare destul de simplă. Tot ce trebuie să facem este să graficăm ecuația pe care am găsit-o eliminând parametrul., După cum sa menționat deja, există două mici probleme cu această metodă. Primul este direcția mișcării. Ecuația care implică numai \(x\) și \(y\) nu va da direcția de mișcare a curbei parametrice. Aceasta este, în general, o problemă ușor de rezolvat cu toate acestea. Să aruncăm o privire rapidă asupra derivatelor ecuațiilor parametrice din ultimul exemplu. Acestea sunt,
\
rețineți că derivata \(x\) nu este la fel de utilă pentru această analiză, deoarece va fi atât pozitivă, cât și negativă și, prin urmare, \(x\) va crește și va scădea în funcție de valoarea lui \(t\)., Acest lucru nu ajută cu direcția de mult ca urmare a curbei în ambele direcții va expune atât în creștere și în scădere \(x\).în unele cazuri, doar una dintre ecuații, cum ar fi acest exemplu, va da direcția, în timp ce în alte cazuri, una ar putea fi utilizată. De asemenea, este posibil ca, în unele cazuri, ambele derivate să fie necesare pentru a determina direcția. Acesta va depinde întotdeauna de setul individual de ecuații parametrice.,
a doua problemă cu eliminarea parametrului este ilustrată cel mai bine într-un exemplu, deoarece vom rula în această problemă în exemplele rămase.
bine, a fost un exemplu foarte lung. Majoritatea acestor tipuri de probleme nu sunt atât de lungi. Am avut doar o mulțime de a discuta în acest unul astfel încât am putea obține o serie de idei importante din drum. Restul exemplelor din această secțiune nu ar trebui să dureze atât de mult.acum, să aruncăm o privire la un alt exemplu care va ilustra o idee importantă despre ecuațiile parametrice.,deci ,am văzut în ultimele două exemple două seturi de ecuații parametrice care într-un fel au dat același grafic. Cu toate acestea, pentru că au urmărit graficul de un număr diferit de ori, chiar trebuie să ne gândim la ele ca la curbe parametrice diferite, cel puțin într-un fel. Aceasta poate părea o diferență de care nu trebuie să ne facem griji, dar, după cum vom vedea în secțiunile ulterioare, aceasta poate fi o diferență foarte importantă. În unele dintre secțiunile ulterioare vom avea nevoie de o curbă care este urmărită exact o dată.,
înainte de a trece la alte probleme să recunoaștem pe scurt ce se întâmplă prin schimbarea \(t\) la un nt în aceste tipuri de ecuații parametrice. Când avem de-a face cu ecuații parametrice care implică numai sines și cosinus și ambele au același argument dacă schimbăm argumentul de la \(t\) la nt, schimbăm pur și simplu viteza cu care curba este trasată. Dacă \(n > 1\) vom crește viteza și dacă \(n < 1\) vom micșora viteza.să aruncăm o privire la câteva exemple.,
până în acest moment am văzut exemple care ar urmări graficul complet pe care l-am obținut eliminând parametrul dacă am lua o gamă suficient de mare de \(t\). cu toate acestea, în exemplul anterior am văzut acum că acest lucru nu va fi întotdeauna cazul. Este mai mult decât posibil de a avea un set de ecuații parametrice, care va urmări în mod continuu doar o porțiune a curbei. De obicei, putem determina dacă acest lucru se va întâmpla căutând limite pe \(x\) și \(y\) care ne sunt impuse de ecuația parametrică.,vom folosi adesea ecuații parametrice pentru a descrie calea unui obiect sau a unei particule. Să aruncăm o privire la un exemplu în acest sens.
ar trebui să dăm un mic avertisment în acest moment. Din cauza ideilor implicate în ele ne-am concentrat pe curbele parametrice care au retras porțiuni ale curbei de mai multe ori. Nu, totuși, prea blocat în ideea că acest lucru se va întâmpla întotdeauna. Multe, dacă nu cele mai multe curbe parametrice vor urmări doar o singură dată. Primul la care ne-am uitat este un bun exemplu în acest sens. Acea curbă parametrică nu va repeta niciodată nicio porțiune din ea însăși.,
există un subiect final care trebuie discutat în această secțiune înainte de a trece mai departe. Până acum am început cu ecuații parametrice și am eliminat parametrul pentru a determina curba parametrică.cu toate acestea, există momente în care vrem să mergem invers. Având în vedere o funcție sau o ecuație, am putea dori să notăm un set de ecuații parametrice pentru aceasta. În aceste cazuri spunem că parametrizăm funcția.dacă luăm exemplele 4 și 5 ca exemple, putem face acest lucru pentru elipse (și, prin urmare, cercuri)., Dat elipsa
\
un set de ecuații parametrice pentru că ar fi,
\
Acest set de ecuații parametrice va trasa elipsa începând de la punctul \(\left( {a,0} \right)\) și va urmări într-un contra-sensul acelor de ceasornic și se va trasa o singură dată în intervalul \(0 \le t \le 2\pi \). Acesta este un set destul de important de ecuații parametrice așa cum este folosit în mod continuu în unele subiecte cu care se ocupă cu elipse și/sau cercuri.fiecare curbă poate fi parametrizată în mai multe moduri. Oricare dintre următoarele va parametriza, de asemenea, aceeași elipsă.,
\
prezența \(\omega \) va schimba viteza pe care o rotește elipsa așa cum am văzut în exemplul 5. Rețineți, de asemenea, că ultimele două vor urmări elipsele în sensul acelor de ceasornic (poate doriți să verificați acest lucru). De asemenea, rețineți că nu vor începe toate în același loc (dacă ne gândim la \(t = 0\) ca punct de plecare care este).
există mult mai multe parametrizări ale unei elipse, desigur, dar ați înțeles ideea. Este important să ne amintim că fiecare Parametrizare va urmări curba o dată cu un interval potențial diferit de \(t\)., Fiecare Parametrizare se poate roti cu direcții diferite de mișcare și poate începe în puncte diferite.este posibil să descoperiți că aveți nevoie de o Parametrizare a unei elipse care începe dintr-un anumit loc și are o anumită direcție de mișcare și astfel știți acum că, cu unele lucrări, puteți scrie un set de ecuații parametrice care vă vor oferi comportamentul pe care îl urmăriți.acum, să notăm câteva alte parametrizări importante și toate comentariile despre direcția de mișcare, punctul de plecare și intervalul \(t\) pentru o singură urmă (dacă este cazul) sunt încă adevărate.,
În primul rând, deoarece un cerc nu este altceva decât un caz special al unei elipse, putem folosi parametrizarea unei elipse pentru a obține ecuațiile parametrice pentru un cerc centrat și la originea razei \(r\). Un posibil mod de a parametriza un cerc este,
\ \
La acest moment se poate părea util să se facă o parametrizare de o funcție ca asta, dar sunt multe cazuri în care acesta va fi de fapt mai ușor, sau poate fi chiar necesară, pentru a lucra cu parametrizarea în loc de funcția în sine., Din păcate, aproape toate aceste cazuri apar într-un curs de calcul III.
















Lasă un răspuns