afișare anunț mobil afișează toate notele ascunde toate notele
Section 4-11: Linear Approximations
În această secțiune vom arunca o privire la o aplicație nu a derivatelor, ci a liniei tangente la o funcție. Desigur, pentru a obține linia tangentă trebuie să luăm derivate, deci într-un fel aceasta este și o aplicație a derivatelor.
\
aruncați o privire la următorul grafic al unei funcții și al liniei sale tangente.
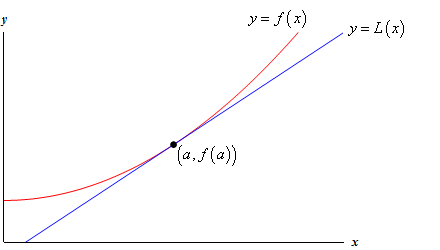
deci, de ce am face asta? Să aruncăm o privire la un exemplu.,
aproximările liniare fac o treabă foarte bună de aproximare a valorilor lui \(f\left( x \right)\) atâta timp cât rămânem „aproape” \(x = a\). Cu toate acestea, mai departe de \(x = a\) vom obține mai rău aproximarea este susceptibil de a fi. Principala problemă aici este că cât de aproape trebuie să rămânem la \(x = a\) pentru a obține o aproximare bună va depinde atât de funcția pe care o folosim, cât și de valoarea lui \(x = a\) pe care o folosim. De asemenea, de multe ori nu va exista o modalitate ușoară de a prezice cât de departe de \(x = a\) putem obține și încă mai avem o aproximare „bună”.,să aruncăm o privire la un alt exemplu care este de fapt folosit destul de puternic în unele locuri.aceasta este de fapt o aproximare liniară oarecum importantă. În optică, această aproximare liniară este adesea folosită pentru a simplifica formulele. Această aproximare liniară este, de asemenea, utilizată pentru a ajuta la descrierea mișcării unui pendul și a vibrațiilor într-un șir.
















Lasă un răspuns