rădăcinile unui polinom

o rădăcină sau zero a unei funcții este un număr care, atunci când este conectat pentru variabilă, face funcția egală cu zero. Astfel, rădăcinile unui polinom P (x) sunt valori ale lui x astfel încât P(x) = 0.

Teorema zerourilor raționale

Teorema zerourilor raționale afirmă:

putem folosi teorema zerourilor raționale pentru a găsi toate zerourile raționale ale unui polinom., Iată pașii:

  1. aranjați polinomul în ordine descrescătoare
  2. notați toți factorii termenului constant. Acestea sunt toate valorile posibile ale lui p.
  3. notați toți factorii coeficientului principal. Acestea sunt toate valorile posibile ale q.
  4. notați toate valorile posibile ale . Amintiți-vă că de factori pot fi negative, și trebuie să fie incluse. Simplificați fiecare valoare și traversați orice duplicate.,
  5. Utilizarea sintetice divizia a determina valorile pentru care P() = 0. Acestea sunt toate rădăcinile raționale ale lui P (x).exemplu: găsiți toate zerourile raționale ale lui P (x) = x3-9x + 9 + 2×4-19×2.

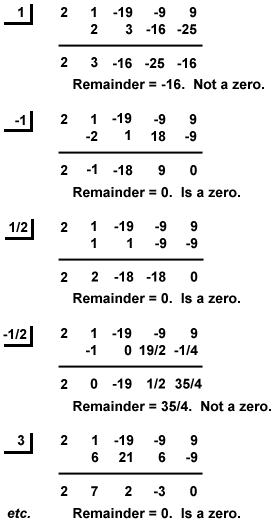
    Figura %: Sintetic Diviziune

    Astfel, rațională rădăcinile lui P(x) x = – 3, -1, 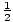, și 3.

    putem folosi adesea teorema zerourilor raționale pentru a factor un polinom., Folosind diviziunea sintetică, putem găsi o rădăcină reală a și putem găsi coeficientul când P (x) este împărțit la x – A. apoi, putem folosi diviziunea sintetică pentru a găsi un factor al coeficientului. Putem continua acest proces până când polinomul a fost complet luat în calcul.