Un vecteur a la grandeur (combien de temps) et de la direction:
Voici deux vecteurs:

Ils peuvent être multipliés à l’aide de la « Produit scalaire » (voir également le Produit vectoriel).,
On peut calculer le Produit scalaire de deux vecteurs de cette façon:

a · b = |a| × |b| × cos(θ)
Où:
|a| est la grandeur (longueur) de vecteur
|b| est la grandeur (longueur) du vecteur b
θ est l’angle entre a et b
nous avons Donc multiplier la longueur d’une fois la longueur de b, puis multiplier par le cosinus de l’angle entre a et b
OU on peut le calculer de cette façon:
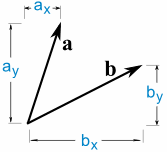
a · b = ax × bx + ay × par
on multiplie Donc les x, multiplier les de y, puis sur ajouter.,
les Deux méthodes de travail!
Et le résultat est un nombre (appelé un « scalaire » donc nous savons que ce n’est pas un vecteur).
Remarque: Vous pouvez utiliser le calcul vectoriel pour vous aider.
Pourquoi cos(θ) ?
OK, pour multiplier deux vecteurs, il est logique de multiplier leurs longueurs ensemble mais seulement quand ils pointent dans la même direction.,
Donc, nous faisons un point dans le même sens que les autres en multipliant par cos(θ):
 |
 |
|
| Nous prenons la composante d’un qui se trouve à côté de b |
Comme une lumière pour voir où l’ombre se trouve |
ENSUITE, on multiplie !,
angles droits
lorsque deux vecteurs sont perpendiculaires l’un à l’autre, le produit scalaire est nul.
Cela peut être un moyen pratique pour savoir si deux vecteurs sont à angle droit.
trois Dimensions ou plus
tout cela fonctionne très bien dans 3 dimensions (ou plus), aussi.
et peut en fait être très utile!
j’ai essayé un calcul comme celui-là une fois, mais j’ai travaillé tous dans les angles et les distances … c’était très dur, impliquait beaucoup de trigonométrie et mon cerveau me faisait mal. La méthode ci-dessus est beaucoup plus facile.,
produit croisé
Le produit Dot donne une réponse scalaire (nombre ordinaire), et est parfois appelé le produit scalaire.
Mais il y a aussi le produit croisé qui donne un vecteur comme réponse, et est parfois appelé le produit vectoriel.

















Laisser un commentaire