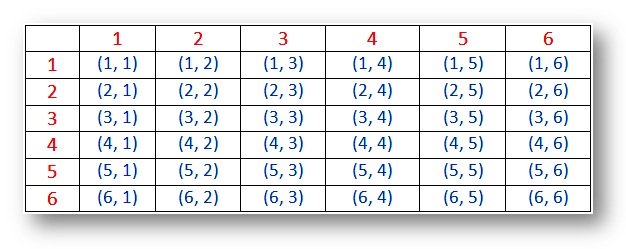
Probabilité de lancer deux dés

Probabilité de lancer deux dés avec les points à six faces tels que 1, 2, 3, 4, 5 et 6 points dans chaque dé.

lorsque deux dés sont lancés simultanément, le nombre d’événement peut donc être 62 = 36 car chaque dé a un nombre de 1 à 6 sur ses faces. Ensuite, les résultats possibles sont présentés dans le tableau ci-dessous.,

Probabilité de l’Échantillon de l’espace pour les deux dés (résultats):

Note:

(i) Les résultats (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) et (6, 6) sont des doublets.

(ii) La paire (1, 2) et (2, 1) sont des résultats différents.

problèmes élaborés impliquant la probabilité de lancer deux dés:

1. Deux dés sont lancés. Soit A, B, C les événements de l’obtention d’une somme de 2, une somme de 3 et une somme de 4, respectivement., Ensuite, montrer que

(i) A est un événement simple

(ii) B et C sont des composés événements

(iii) A et B sont mutuellement exclusifs

la Solution:

Clairement, nous avons
A = {(1, 1)}, B = {(1, 2), (2, 1)} et C = {(1, 3), (3, 1), (2, 2)}.

(I) puisque A se compose d’un seul point d’échantillon, c’est un événement simple.

(ii) puisque B et C contiennent plus d’un point d’échantillon, chacun d’eux est un événement composé.

(iii) puisque A B B = ∅, A et B s’excluent mutuellement.

2. Deux dés sont lancés., Un événement que la somme des nombres figurant dans les deux dés est de 5, et B est l’événement qu’au moins l’un des dés montre un 3.
Les deux événements (i) s’excluent-ils mutuellement, (ii) sont-ils exhaustifs? Donnez des arguments à l’appui de votre réponse.

la Solution:

Quand les deux dés sont lancés, nous avons n(S) = (6 × 6) = 36.

Maintenant, Un = {(1, 4), (2, 3), (4, 1), (3, 2)}, et

B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}

(i) A ∩ B = {(2, 3), (3, 2)} ≠ ∅.

Par conséquent, A et B ne sont pas mutuellement exclusifs.,

(ii) Également, A B B ≠ S.

Par conséquent, A et B ne sont pas des événements exhaustifs.

Plus d’exemples se rapportant aux questions sur les probabilités pour lancer deux dés.

3. Deux dés sont lancés simultanément.,) l’obtention d’un doublet

(v) l’obtention d’une somme de 8

(vi) prise en somme divisible par 5

(vii) l’obtention d’une somme d’au moins 11

(viii) l’obtention d’un multiple de 3 comme la somme

(ix) d’obtenir un total d’au moins 10

(x) obtenir un nombre pair comme la somme

(xi) l’obtention d’un nombre premier comme la somme

(xii) l’obtention d’un doublet de même les nombres

(xiii) l’obtention d’un multiple de 2 sur un dé et un multiple de 3 sur l’autre mourir

la Solution:

Deux dés sont lancés simultanément être le numéro 1, 2, 3, 4, 5 et 6 sur leurs visages., Nous savons que dans un seul lancer de deux dés différents, le nombre total de résultats possibles est (6 × 6) = 36.

(I) obtenir six en tant que produit:

Let E1 = événement d’obtenir six en tant que produit. Le nombre dont le produit est six sera E1 = = 4

par conséquent, probabilité d’obtenir ‘six comme produit’

nombre de résultats favorables
P(E1) = nombre Total de résultats possibles
= 4/36
= 1/9

(ii) obtenir une somme ≤ 3:

soit E2 = événement d’obtenir une somme ≤ 3., Le nombre dont la somme ≤ 3 sera E2 = = 3

par conséquent, probabilité d’obtenir ‘somme ≤ 3’

nombre de résultats favorables
P(E2) = nombre Total de résultats possibles
= 3/36
= 1/12

(iii) obtenir somme ≤ 10:

soit E3 = événement d’obtenir somme ≤ 10. Le nombre dont la somme ≤ 10 sera E3 =

= 33

par conséquent, probabilité d’obtenir ‘somme ≤ 10’

nombre de résultats favorables
P(E3)= nombre Total de résultats possibles
= 33/36
= 11/12
(iv)obtenir un doublet:soit E4 = événement d’obtenir un doublet., Le nombre dont le doublet sera E4 = = 6

par conséquent, probabilité d’obtenir ‘un doublet’

nombre de résultats favorables
P(E4) = nombre Total de résultats possibles
= 6/36
= 1/6

(v)obtenir une somme de 8:

soit E5 = événement d’obtenir une somme de 8. Le nombre qui est une somme de 8 sera E5 = = 5

par conséquent, la probabilité ofgetting ‘une somme de 8’

le Nombre de résultats favorables
P(E5) = nombre Total de résultats possibles
= 5/36

(vi)prise en somme divisible par 5:

Laissez-E6 = événement de prise en somme divisible par 5., Le nombre dont la somme divisible par 5 sera E6 = = 7

par conséquent, probabilité d’obtenir ‘somme divisible par 5’

nombre de résultats favorables
P(E6) = nombre Total de résultats possibles
= 7/36

(vii)obtenir la somme d’au moins 11:

soit E7 = événement d’obtenir la somme d’au moins 11. Les événements de la somme d’au moins 11 sera E7 = = 3

par conséquent, la probabilité ofgetting  » somme d’au moins 11’

le Nombre de résultats favorables
P(E7) = nombre Total de résultats possibles
= 3/36
= 1/12

(viii) mise en amultiple de 3 comme la somme:

Laissez-E8 = événement d’obtenir un multiple de 3 car la somme., Les événements d’un multiple de 3 comme somme seront E8 = = 12

par conséquent, probabilité d’obtenir ‘un multiple de 3 comme somme’

nombre de résultats favorables
P(E8) = nombre Total de résultats possibles
= 12/36
= 1/3

(ix) obtenir un totalof au moins 10:

soit E9 = événement d’obtenir un total d’au moins 10., Les événements d’un total d’au moins 10 seront E9 = = 6

par conséquent, probabilité d’obtenir ‘un total d’au moins 10’

nombre de résultats favorables
P(E9) = nombre Total de résultats possibles
= 6/36
= 1/6

(x) obtenir un nombre égal comme somme:

soit E10 = événement d’obtenir un nombre pair comme somme., Les événements d’un nombre pair comme somme seront E10 = = 18

par conséquent, probabilité d’obtenir un nombre pair comme somme

nombre de résultats favorables
P(E10) = nombre Total de résultats possibles
= 18/36
= 1/2

(xi) obtenir un nombre premier comme somme:

soit E11 = événement d’obtenir un nombre premier comme somme., Les événements d’un nombre premier comme somme seront E11 = = 15

par conséquent, probabilité d’obtenir ‘un nombre premier comme somme’

nombre de résultats favorables
P(E11) = nombre Total de résultats possibles
= 15/36
= 5/12

(xii) obtenir un doublet de nombres pairs:

soit E12 = événement d’obtenir un doublet de nombres pairs., Les événements d’un doublet de même les nombres seront E12 = = 3

par conséquent, la probabilité ofgetting ‘un doublet de même les nombres’

le Nombre de résultats favorables
P(E12) = nombre Total de résultats possibles
= 3/36
= 1/12

(xiii) se amultiple de 2 sur un dé et un multiple de 3 sur l’autre mourir:

Laissez-E13 = cas de l’obtention d’un multiple de 2 sur un dé et un multiple de 3 sur l’autre mourir., Les événements d’un multiple de 2 sur un dé et un multiple de 3 sur l’autre mourir seront E13 = = 11

par conséquent, la probabilité ofgetting ‘un multiple de 2 sur un dé et un multiple de 3 sur l’autre mourir  »

le Nombre de résultats favorables
P(E13) = nombre Total de résultats possibles
= 11/36

4. Twodice sont jetés. Trouvez (i) les chances en faveur de l’obtention de la somme 5, et (ii) les chances contre l’obtention de la somme 6.

Solution:

nous savons que dans un seul lancer de deux dé, le nombre total de résultats possibles est (6 × 6) = 36.

soit S l’exemple de l’espace. Ensuite, n (S) = 36.,

(i) les chances d’obtenir la somme 5:

soit E1 l’événement d’obtenir la somme 5. Alors,
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒ P(E1) = 4
par conséquent, P(E1) = n(E1)/n(S) = 4/36 = 1/9
⇒ la cote en faveur de E1 = P(E1)/ = (1/9)/(1 – 1/9) = 1/8.

(ii) les chances d’obtenir la somme 6:

soit E2 l’événement d’obtenir la somme 6. Alors,
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒ P(E2) = 5
par conséquent, P(E2) = n(E2)/n(S) = 5/36
⇒ chances contre E2 = /P(E2) = (1 – 5/36)/(5/36) = 31/5.

5., Deux dés, un bleu et un orange, sont lancés simultanément. Trouver la probabilité d’obtenir

(i) un nombre égal sur les deux

(ii) deux numéros dont la somme est 9.,

la Solution:

Les résultats possibles sont:

(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)

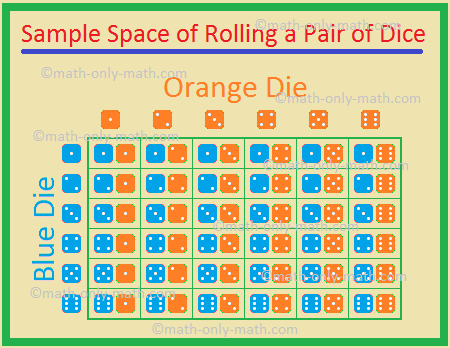
par conséquent, le nombre total de résultats possibles = 36.,

(i) le Nombre de résultats favorables pour l’événement E

= nombre de résultats ayant un nombre égal sur les deux dés

= 6 .

Donc, par définition, P(E) = \(\frac{6}{36}\)

= \(\frac{1}{6}\)

(ii) Nombre de résultats favorables pour l’événement F

= Nombre de résultats dans laquelle deux numéros ont sur eux la somme de 9

= 4 .

Donc, par définition, P(F) = \(\frac{4}{36}\)

= \(\frac{1}{9}\).

Ces exemples nous aideront à résoudre différents types de problèmes basés sur la probabilité de lancer deux dés.,p>Probability and Playing Cards

Probability for Rolling Two Dice

Solved Probability Problems

Probability for Rolling Three Dice

9th Grade Math

From Probability for Rolling Two Dice to HOME PAGE