aller à la surface ou au Volume.
un prisme est Un objet solide avec:
- identiques se termine
- faces plates
- et la même section transversale tout au long de sa longueur !
une section transversale est la forme faite en coupant directement à travers un objet.
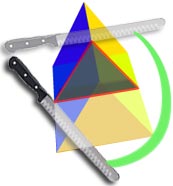
La section transversale de cet objet est un triangle …
.. il a la même section transversale sur toute sa longueur …
… c’est donc un prisme triangulaire.,
|
Essayer de dessiner une forme sur un morceau de Alors imaginer l’extension de la feuille de papier … |
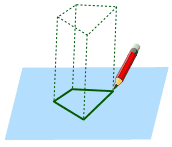 |
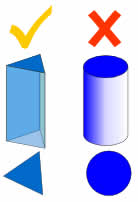
Pas de Courbes!
Un prisme est un polyèdre, ce qui signifie que toutes les faces sont plates!
Pas de côtés incurvés.
Par exemple, un cylindre n’est pas un prisme, parce qu’il a des côtés courbes.,
les Bases
Les extrémités d’un prisme sont parallèles
et chacun est appelé base.
les Côtés
Les faces latérales du prisme sont des parallélogrammes
(4-verso des formes avec des côtés opposés parallèles)
ce sont tous des Prismes:
et plus encore!

Exemple: Ce hexagonale du cristal de glace.
Il ressemble à un hexagone, mais parce qu’il a une certaine épaisseur, il est en fait un prisme hexagonal!
Photographie de la NASA / Alexey Kljatov.,
prismes réguliers vs irréguliers
tous les exemples précédents sont des prismes réguliers, car la section transversale est régulière (en d’autres termes, c’est une forme avec des longueurs de bord égales et des angles égaux.,)
Here is an example of an Irregular Prism:
| Irregular Pentagonal Prism: | ||
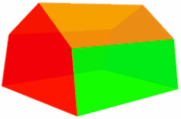 |
 |
|
| Cross-Section | ||
| It is « irregular » because the cross-section is not « regular » in shape.,div> Surface = 2 × Superficie de Base
+ Base de Périmètre × Durée Exemple: Quelle est la surface d’un prisme où la superficie de base est de 25 m2, le périmètre de la base est de 24 m, et la longueur est de 12 m: Surface = 2 × Superficie de Base de Base + Périmètre × Durée
= 2 × 25 m2 + 24 m × 12 m
= 50 m2 + 288 m2
= 338 m2
(Note: nous avons une Zone de Calcul de l’Outil) le Volume d’un PrismeLe Volume d’un prisme est la superficie de la fin des temps de la longueur du prisme., Volume = Aire de Base × Durée Exemple: Quel est le volume d’un prisme où la superficie de base est de 25 m2 et de 12 m de long: Volume = Aire × Durée
= 25 m2 × 12 m
= 300 m3
Jouer avec elle ici., La formule fonctionne aussi quand il « penche » (oblique), mais rappelez-vous que la hauteur est perpendiculaire à la base: Et c’est pourquoi:
© 2021 Tombouctou Theme by Anders Noren — Up ↑ | ||






















Laisser un commentaire