zawartość (Kliknij, aby przejść do tej sekcji):
- wszystko o…
- Średnia
- tryb
- mediana
- jak ręcznie znaleźć średnią, medianę i tryb.
- Znajdź średnią, medianę i tryb za pomocą technologii:
- SPSS
- TI83
przegląd
Jak znaleźć średnią, medianę,& tryb w statystykach?,
- średnia jest średnią zbioru danych.
- tryb jest najczęstszą liczbą w zbiorze danych.
- mediana jest środkiem zbioru liczb.
z tych trzech, średnia jest jedyną, która wymaga wzoru. Lubię myśleć o tym w innym słownikowym znaczeniu tego słowa (jak w, to znaczy w przeciwieństwie do Nicei!). To dlatego, że w porównaniu do dwóch pozostałych nie jest tak łatwo pracować.,
wskazówki do zapamiętania różnicy
masz problemy z zapamiętaniem różnicy między średnią, medianą i trybem? Oto kilka wskazówek, które mogą pomóc. Możesz również sprawdzić korepetycje w Chegg.com (pierwsze 30 minut za darmo!).
- „a la mode” to francuskie słowo oznaczające modny ; odnosi się również do popularnego sposobu serwowania lodów. Tak więc „moda” jest najbardziej popularnym lub modnym członkiem zbioru liczb. Tryb słowa jest również jak większość.,
- „Średnia” wymaga arytmetyki (dodawania wszystkich liczb i dzielenia) , więc jest to „średnia”.
- „Mediana” ma taką samą liczbę liter jak”środek”.
nadal nie jesteś pewien, jaka jest różnica między tymi trzema? Obejrzyj film lub czytaj dalej, aby uzyskać więcej informacji:
Średnia
Średnia vs. Mediana
Średnia vs., Średnia
specyficzne „środki” powszechnie stosowane w Stats
inne typy
Średnia vs Mediana
oba są miary, gdzie znajduje się środek zbioru danych (zwany „tendencja Centralna” w stats), ale są one zwykle różne liczby. Na przykład, weźmy tę listę liczb: 10, 10, 20, 40, 70.
- średnia (nieformalnie „średnia”) znajduje się przez dodanie wszystkich liczb razem i podzielenie przez liczbę elementów w zbiorze: 10 + 10 + 20 + 40 + 70 / 5 = 30.
- mediana znajduje się poprzez uporządkowanie zbioru od najniższego do najwyższego i znalezienie dokładnego środka., Mediana to tylko środkowa liczba: 20.
czasami te dwa będą tymi samymi liczbami. Na przykład zbiór danych 1, 2, 4, 6, 7 ma średnią 1 + 2 + 4 + 6 + 7 / 5 = 4 i mediana (środek) 4.
Średnia vs Średnia: Jaka jest różnica?
kiedy zaczynałeś naukę matematyki, prawdopodobnie nauczyłeś się, że średnia jest” średnią ” dla zbioru liczb. Dodałeś liczby, podzielone przez liczbę przedmiotów, które możesz i voila! dostajesz średnią. Na przykład średnia 10, 5 i 20 wynosi:
10 + 6 + 20 = 36 / 3 = 12.,
zacząłeś studiować statystyki i nagle „średnia” nazywa się teraz średnią. Co się stało? Odpowiedź jest taka, że mają to samo znaczenie (są synonimami).
mówiąc technicznie, słowo mean jest skrótem od średniej arytmetycznej. Używamy różnych słów w statystykach, ponieważ istnieje wiele różnych rodzajów środków i wszystkie one robią różne rzeczy.
specyficzne „środki” powszechnie używane w statystykach
prawdopodobnie natkniesz się na nie w swojej klasie statystyk., Mają bardzo wąskie znaczenia:
- Średnia rozkładu próbkowania: używany z rozkładami prawdopodobieństwa, zwłaszcza z centralnym twierdzeniem granicznym. To średnia ze zbioru rozkładów.
- Średnia próbka: Średnia wartość w próbce.
- średnia liczba ludności: Średnia wartość w populacji.
1, 3rd ed. Princeton, NJ: Van Nostrand, 1962.
inne rodzaje
istnieją inne rodzaje środków i będziesz ich używać w różnych gałęziach matematyki., Większość ma bardzo wąskie zastosowania do dziedzin takich jak finanse czy fizyka; jeśli jesteś w elementarnych statystykach, prawdopodobnie nie będziesz z nimi pracować.
to jedne z najczęściej spotykanych typów.
- średnia ważona.
- średnia harmoniczna.
- średnia geometryczna.
- średnia arytmetyczno-geometryczna.
- Root-Średnia kwadratowa średnia.
- Heronian mean.
- Średnia graficzna
-
średnia ważona
są one dość powszechne w statystykach, szczególnie podczas badania populacji., Zamiast każdego punktu danych przyczyniających się w równym stopniu do średniej końcowej, niektóre punkty danych przyczyniają się w większym stopniu niż inne. Jeśli wszystkie wagi są równe, to będzie równa średniej arytmetycznej. Istnieją pewne okoliczności, w których może to dać błędne informacje, na co wskazuje paradoks Simpsona.
-
Średnia harmoniczna
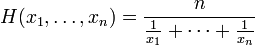
wzór harmoniczny.
aby go znaleźć:
- Dodaj odwrotność liczb w zbiorze., Aby znaleźć odwrotność, Odwróć ułamek tak, aby licznik stał się mianownikiem, a mianownik stał się licznikiem. Na przykład odwrotność 6/1 wynosi 1/6.
- podziel odpowiedź przez liczbę pozycji w zestawie.
- weź odwrotność wyniku.
średnia harmoniczna jest dość często używana w fizyce. W niektórych przypadkach z udziałem stawek i wskaźników daje lepszą średnią niż średnia arytmetyczna. Znajdziesz tu również zastosowania w geometrii, finansach i informatyce.,
-
średnia geometryczna
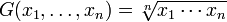
ten typ ma bardzo wąskie i Specyficzne zastosowania w finansach, naukach społecznych i technologii. Załóżmy na przykład, że posiadasz akcje, które zarabiają 5% w pierwszym roku, 20% w drugim roku i 10% w trzecim roku. Jeśli chcesz znać średnią stopę zwrotu, nie możesz użyć średniej arytmetycznej. Dlaczego? Bo kiedy znajdujesz stopy zwrotu, to mnożysz, a nie dodajesz. Na przykład w pierwszym roku mnożą się przez 1,05., -
Średnia arytmetyczno-geometryczna
jest używana głównie w obliczeniach matematycznych i w obliczeniach maszynowych (tj. jako podstawa wielu obliczeń komputerowych). Ma związek z obwodem elipsy. Kiedy został po raz pierwszy opracowany przez Gaussa, był używany do obliczania Orbit planetarnych. Arytmetyczno-geometryczny jest (nic dziwnego!) mieszanka średnich arytmetycznych i geometrycznych. Matematyka jest dość skomplikowana, ale można znaleźć stosunkowo proste wyjaśnienie matematyki tutaj.,
-
Root-średni kwadrat
jest bardzo przydatny w dziedzinach, które badają fale sinusoidalne, takich jak Elektrotechnika. Ten szczególny typ jest również nazywany średnią kwadratową. Zobacz: Średnia Kwadratowa / Średnia Kwadratowa.
-
Heronian Mean
używany w geometrii do znalezienia objętości Piramidalnej frustum. Piramidalna frustum to w zasadzie piramida z odciętym wierzchołkiem.
-
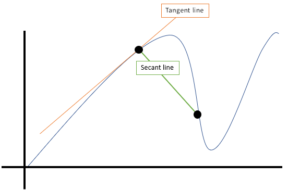
graficzna Średnia
inna nazwa nachylenia linii sekantu: odpowiednik średniego tempa zmian między dwoma punktami.,
Co to jest tryb?
tryb jest najczęstszą liczbą w zbiorze. Na przykład tryb w tym zbiorze liczb wynosi 21:
21, 21, 21, 23, 24, 26, 26, 28, 29, 30, 31, 33
Jaka jest mediana?
mediana jest liczbą środkową w zbiorze danych. Aby znaleźć medianę, wymień punkty danych w porządku rosnącym, a następnie znajdź środkową liczbę., Liczba Środkowa w tym zbiorze to 28, ponieważ pod nim są 4 cyfry i 4 cyfry powyżej:
23, 24, 26, 26, 28, 29, 30, 31, 33
jak znaleźć średnią, medianę i tryb ręcznie: kroki
Jak znaleźć średnią, medianę i tryb: tryb
Jak znaleźć średnią, medianę i tryb: średnia
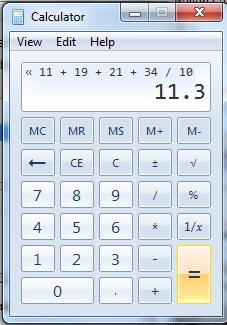
dzieląc sumę przez liczbę pozycji, aby znaleźć średnią.
Jak znaleźć średnią, medianę i tryb: mediana
Jeśli masz nieparzystą liczbę w kroku 3, Przejdź do kroku 5. Jeśli masz numer parzysty, przejdź do kroku 6.,
Wskazówka: Możesz mieć więcej niż jeden tryb. Na przykład tryb 1, 1, 5, 5, 6, 6 1, 5 i 6.
podoba Ci się Wyjaśnienie? Sprawdź Podręcznik statystyki praktycznie oszustwa, który zawiera setki innych rozwiązań krok po kroku, takich jak ten!
mediana trybu średniego SPSS
aby znaleźć medianę trybu średniego SPSS, musisz użyć zakładki Częstotliwość. Wydaje się to nieco sprzeczne z intuicją, ale Zakładka statystyki opisowe nie daje opcji znalezienia trybu lub mediany.,
SPSS ma bardzo podobny interfejs do Microsoft Excel. Dlatego jeśli korzystałeś wcześniej z programu Microsoft Excel, szybko dostosujesz się do SPSS.
tryb średni SPSS Mediana: kroki
Obejrzyj film lub przeczytaj poniższe kroki:
przykładowe pytanie: Znajdź medianę trybu SPSS dla następującego zestawu danych: 20,23,35,66,55,66
Krok 1: Otwórz SPSS. W „co chciałbyś zrobić?”okno dialogowe, kliknij przycisk radiowy „wpisz dane”, a następnie kliknij ” OK.”Otworzy się nowy arkusz roboczy., Uwaga: jeśli zrezygnowałeś z pierwszego ekranu pomocy, Ta opcja może nie być widoczna. W takim razie zacznij od kroku 2.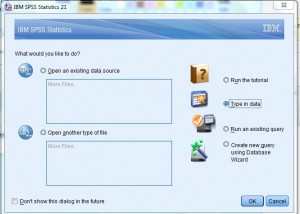
Krok 2: Wpisz swoje dane do arkusza roboczego. Dane można wpisać do jednej kolumny lub wielu kolumn, jeśli masz wiele zestawów danych. W tym przykładzie wpisz 20, 23, 35, 66, 55, 66 do kolumny 1. Nie zostawiaj spacji między danymi (tzn. nie zostawiaj pustych wierszy).
Krok 2: Kliknij „Analizuj”, najedź kursorem na” statystyki opisowe”, a następnie kliknij ” częstotliwości.,”
Krok 3: Kliknij „Statystyki”, a następnie zaznacz pola „mean”, „mode” i ” mediana.”Kliknij” Kontynuuj „dwukrotnie (wybierz „Brak” jako typ wykresu w drugim oknie).
Uwaga: w niektórych wersjach SPSS może być konieczne tylko jedno kliknięcie „Kontynuuj” i może nie dać ci opcji typu wykresu.
wyniki częstotliwości pojawią się jako wynik. Górna część wyjścia wyświetli średnią, tryb i medianę.
Jeśli przewiń w dół, Tabela częstotliwości wyświetli również tryb., Tryb definiowany jest w statystykach jako Liczba o najwyższej częstotliwości (dla tego przykładowego zestawu danych liczba pojawiająca się najczęściej to 66, Z dwoma wynikami w kolumnie częstotliwość).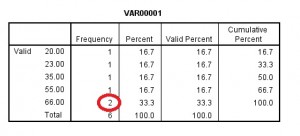
TI 83 średnia, mediana i tryb
znalezienie średniej TI 83 lub mediany TI 83 z listy danych można wykonać na dwa sposoby: wprowadzając listę danych lub wpisując polecenia za pomocą ekranu głównego., Korzystanie z funkcji listy jest tak samo proste, jak wprowadzanie danych na ekranie głównym, a dodatkową zaletą jest to, że możesz użyć danych do innych celów po obliczeniu średniej, trybu i mediany (na przykład możesz utworzyć histogram TI 83).
kroki dla średniej, mediany i trybu na TI 83
Obejrzyj film dla średniej i mediany lub przeczytaj kroki poniżej (tryb, patrz ta uwaga):
Krok 1: Wprowadź powyższe dane do listy., Naciśnij przycisk STAT, a następnie naciśnij ENTER. Wprowadź pierwszą liczbę (1250), a następnie naciśnij ENTER. Kontynuuj wprowadzanie numerów, naciskając przycisk ENTER po każdym wpisie.
Krok 2: Naciśnij przycisk STAT.
Krok 3: Naciśnij przycisk strzałki w prawo, aby wyróżnić „Calc.”
Krok 4: naciśnij ENTER, aby wybrać „1-Var Stats”, a następnie wpisz nazwę listy. Na przykład, aby wejść do L1 Naciśnij i .
Krok 5: naciśnij ENTER ponownie. Kalkulator zwróci średnią, x. Dla tej listy danych średnia TI 83 wynosi 884,05 stóp (zaokrąglona do 3 miejsc po przecinku).
Krok 6: Strzałka w dół, aż zobaczysz „Med.,”Jest to mediana TI 83; dla powyższych danych mediana wynosi 813,05 stóp.
Uwaga: TI-83 plus nie ma wbudowanej funkcji trybu, ale po wprowadzeniu listy łatwo jest rozpoznać tryb: to tylko numer, który występuje najczęściej w zestawie. Nie jesteś pewien? Przeczytaj więcej o tym trybie tutaj.
To jest to!
zgubiłeś przewodnik? Pobierz Nowy tutaj na stronie TI.
> ——————————————————————————
potrzebujesz pomocy w zadaniu domowym lub pytaniu testowym?, Dzięki badaniu Chegg możesz uzyskać krok po kroku rozwiązania swoich pytań od eksperta w tej dziedzinie. Twoje pierwsze 30 minut z korepetytorem Chegg jest bezpłatne!
















Dodaj komentarz