wektor ma wielkość (długość) i kierunek:
oto dwa wektory:

można je pomnożyć za pomocą „produktu kropkowego” (Zobacz także produkt krzyżowy).,
możemy obliczyć iloczyn punktowy dwóch wektorów w ten sposób:

a · b = |a| × |b| × cos(θ)
Gdzie:
|a| jest wielkością (długością) wektora a
|b| jest wielkością (długością) wektora b
θ jest kątem między A i b
więc mnożymy Długość a razy długość B, następnie pomnożymy przez cosinus kąta między A i b
lub możemy obliczyć go w ten sposób:
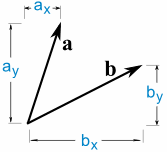
a · b = AX × BX + ay × przez
więc mnożymy x, mnożymy y, a następnie dodajemy.,
obie metody działają!
a wynikiem jest liczba (nazywana „skalarem”, więc wiemy, że nie jest wektorem).
Uwaga: możesz skorzystać z kalkulatora wektorowego.
dlaczego cos(θ) ?
OK, aby pomnożyć dwa wektory warto pomnożyć ich długości razem, ale tylko wtedy, gdy wskazują w tym samym kierunku.,
więc robimy jeden „punkt w tym samym kierunku” co drugi, mnożąc przez cos(θ):
 |
 |
|
| bierzemy składnik a który leży obok b |
jak świeci światło, aby zobaczyć Gdzie Shadow lies |
następnie mnożymy !,
kąty proste
gdy dwa wektory są względem siebie pod kątem prostym, iloczyn punktowy wynosi zero.
To może być przydatny sposób, aby dowiedzieć się, czy dwa wektory są pod kątem prostym.
trzy lub więcej wymiarów
To wszystko działa dobrze w 3 (lub więcej) wymiarach, zbyt.
i rzeczywiście może być bardzo przydatny!
próbowałem kiedyś takiego obliczenia, ale wszystko działało pod kątem i odległościami … to było bardzo trudne, wymagało dużo trygonometrii, i mój mózg bolał. Powyższa metoda jest znacznie łatwiejsza.,
iloczyn krzyżowy
iloczyn punktowy daje odpowiedź skalarną (liczbę zwykłą) i jest czasami nazywany iloczynem skalarnym.
ale istnieje też iloczyn krzyżowy, który daje wektor jako odpowiedź i jest czasami nazywany iloczynem wektorowym.

















Dodaj komentarz