prawdopodobieństwo wyrzucenia dwóch kości

prawdopodobieństwo-przykładowa przestrzeń dla dwóch kości (wyników):

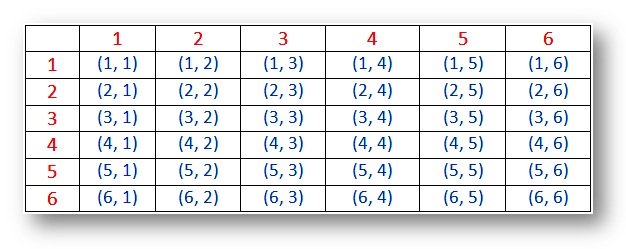
Uwaga:

(i) wyniki(1, 1), (2, 2), (3, 3), (4, 4), (5, 5) i (6, 6) nazywane są dubletami.

rozwiązane problemy dotyczące prawdopodobieństwa rzucenia dwiema kostkami:

1. Rzucono dwie kości. Niech A, B, C będą zdarzeniami otrzymywania odpowiednio Sumy 2, Sumy 3 i Sumy 4., Następnie pokaż, że

(i) A jest zdarzeniem prostym

(ii) B I C są zdarzeniami złożonymi

(iii) a i B wykluczają się wzajemnie

rozwiązanie:

wyraźnie mamy
A = {(1, 1)}, B = {(1, 2), (2, 1)} I C = {(1, 3), (3, 1), (2, 2)}.

(i) Ponieważ A składa się z pojedynczego punktu próbki, jest to zdarzenie proste.

(ii) ponieważ zarówno B jak i C zawierają więcej niż jeden punkt próbki, każdy z nich jest zdarzeniem złożonym.

(iii) ponieważ A ∩ B = ∅, A i B wzajemnie się wykluczają.

2. Rzucono dwie kości., A to zdarzenie, w którym suma liczb pokazanych na dwóch kościach wynosi 5, A B to zdarzenie, w którym co najmniej jedna z kości pokazuje 3.
Czy te dwa zdarzenia (i) wzajemnie się wykluczają, (ii) wyczerpują? Podaj argumenty na poparcie swojej odpowiedzi.

rozwiązanie:

po wyrzuceniu dwóch kostek mamy n (S) = (6 × 6) = 36.

teraz, A = {(1, 4), (2, 3), (4, 1), (3, 2)}, i

B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}

(i) A ∩ B = {(2, 3), (3, 2)} ≠ ∅.

stąd A i B nie wykluczają się wzajemnie.,

(ii) również A ∪ B ≠ S.

dlatego A i B nie są zdarzeniami wyczerpującymi.

więcej przykładów związanych z pytaniami o prawdopodobieństwo rzucania dwiema kostkami.

3. Dwie kości są rzucane jednocześnie.,

(v ) uzyskanie sumy 8

(vi) uzyskanie sumy podzielnej przez 5

(vii) uzyskanie sumy co najmniej 11

(viii) uzyskanie wielokrotności 3 jako sumy

(ix) uzyskanie sumy co najmniej 10

(x) uzyskanie liczby parzystej jako sumy

(Xi) uzyskanie liczby pierwszej jako sumy

(XII) uzyskanie dubletu liczb parzystych

(XIII) uzyskanie wielokrotności 2 na jednej kostce i wielokrotności 3 na drugiej kostce

rozwiązanie:

dwie różne kości są rzucane jednocześnie z numerami 1, 2, 3, 4, 5 i 6 na ich twarzach., Wiemy, że w jednym rzucie dwóch różnych kostek łączna liczba możliwych wyników wynosi (6 × 6) = 36.

(i) getting six as a product:

Let E1 = event of getting six as a product. Liczba, której iloczyn wynosi sześć, będzie E1 = = 4

zatem prawdopodobieństwo uzyskania „sześciu jako iloczynu”

Liczba korzystnych wyników
P(E1) = całkowita liczba możliwych wyników
= 4/36
= 1/9

(ii) uzyskanie Sumy ≤ 3:

niech E2 = Zdarzenie uzyskania sumy ≤ 3., Liczba, której suma ≤ 3 będzie E2 = = 3

zatem prawdopodobieństwo uzyskania „suma ≤ 3”

Liczba korzystnych wyników
P(E2) = całkowita liczba możliwych wyników
= 3/36
= 1/12

(iii) uzyskanie sumy ≤ 10:

niech E3 = Zdarzenie uzyskania sumy ≤ 10. Liczba, której suma ≤ 10 będzie E3 =

= 33

dlatego prawdopodobieństwo uzyskania „sumy ≤ 10”

Liczba korzystnych wyników
P(E3)= całkowita liczba możliwych wyników
= 33/36
= 11/12
(iv)uzyskanie dubletu:niech E4 = Zdarzenie uzyskania dubletu., Liczba, która dublet będzie E4 = = 6

dlatego prawdopodobieństwo uzyskania 'dublet'

Liczba korzystnych wyników
P(E4) = całkowita liczba możliwych wyników
= 6/36
= 1/6

(v)uzyskanie sumy 8:

niech E5 = Zdarzenie uzyskania sumy 8. Liczba, która jest sumą 8 będzie E5 = = 5

zatem prawdopodobieństwo uzyskania 'sumy 8′

Liczba korzystnych wyników
P(E5) = całkowita liczba możliwych wyników
= 5/36

(vi)uzyskanie sumy podzielnej przez 5:

niech E6 = Zdarzenie uzyskania sumy podzielnej przez 5., Liczba, której suma podzielna przez 5 będzie E6 = = 7

zatem prawdopodobieństwo uzyskania sumy podzielnej przez 5

Liczba korzystnych wyników
P(E6) = całkowita liczba możliwych wyników
= 7/36

(vii)uzyskanie sumy co najmniej 11:

niech E7 = Zdarzenie uzyskania sumy co najmniej 11. Zdarzenia sumy przynajmniej 11 będzie E7 = = 3

dlatego prawdopodobieństwo uzyskania 'sumy przynajmniej 11′

Liczba korzystnych wyników
P(E7) = całkowita liczba możliwych wyników
= 3/36
= 1/12

(viii) uzyskanie liczby 3 jako sumy:

niech E8 = Zdarzenie uzyskania wielokrotności 3 jako sumy., Zdarzenia wielokrotności 3 jako sumy będzie E8 = = 12

dlatego prawdopodobieństwo uzyskania 'wielokrotności 3 jako sumy'

Liczba korzystnych wyników
P(E8) = całkowita liczba możliwych wyników
= 12/36
= 1/3

(ix) uzyskanie sumy co najmniej 10:

niech E9 = Zdarzenie uzyskania sumy co najmniej 10., Zdarzenia o sumie co najmniej 10 będą E9 = = 6

dlatego prawdopodobieństwo uzyskania 'sumy co najmniej 10′

Liczba korzystnych wyników
P(E9) = całkowita liczba możliwych wyników
= 6/36
= 1/6

(x) uzyskanie liczby parzystej jako sumy:

niech E10 = Zdarzenie uzyskania liczby parzystej jako sumy., Zdarzenia liczby parzystej jako sumy będzie E10 = = 18

dlatego prawdopodobieństwo znalezienia ' liczby parzystej jako sumy

Liczba korzystnych wyników
P(E10) = całkowita liczba możliwych wyników
= 18/36
= 1/2

(xi) uzyskanie liczby pierwszej jako sumy:

niech E11 = Zdarzenie uzyskania liczby pierwszej jako sumy., Zdarzenia liczby pierwszej jako sumy będzie E11 = = 15

dlatego prawdopodobieństwo uzyskania 'liczby pierwszej jako sumy'

Liczba korzystnych wyników
P(E11) = całkowita liczba możliwych wyników
= 15/36
= 5/12

(xii) uzyskanie podwójnej liczby parzystej:

niech E12 = Zdarzenie uzyskania podwójnej liczby parzystej., Zdarzenia dubletu liczb parzystych będą E12 = = 3

dlatego prawdopodobieństwo uzyskania 'dubletu liczb parzystych'

Liczba korzystnych wyników
P(E12) = całkowita liczba możliwych wyników
= 3/36
= 1/12

(xiii) uzyskanie liczby 2 na jednej matrycy i wielokrotności 3 na drugiej matrycy:

niech E13 = Zdarzenie uzyskania wielokrotności 2 na jednej matrycy i wielokrotności 3 na drugiej matrycy:

2 na jednej matrycy i wielokrotność 3 na drugiej matrycy., Zdarzenia wielokrotności 2 na jednej matrycy i wielokrotności 3 na drugiej matrycy będzie E13 = = 11

dlatego prawdopodobieństwo znalezienia „wielokrotności 2 na jednej matrycy i wielokrotności 3 na drugiej matrycy”

Liczba korzystnych wyników
P(E13) = całkowita liczba możliwych wyników
= 11/36

4. / Align = „left” / Znajdź (i) szanse na uzyskanie Sumy 5, oraz (ii) szanse na uzyskanie sumy 6.

rozwiązanie:

wiemy, że w jednym rzucie z dwóch matryc całkowita liczba możliwych wyników wynosi (6 × 6) = 36.

Niech s będzie przestrzenią próbki. Następnie n (S) = 36.,

(i) kursy na uzyskanie Sumy 5:

niech E1 będzie zdarzeniem uzyskania sumy 5.
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒ p (E1) = 4
zatem P(E1) = n (E1) / N(S) = 4/36 = 1/9
⇒ kursy na rzecz E1 = P (E1)/ = (1/9)/(1 – 1/9) = 1/8.

(ii) szanse na uzyskanie sumy 6:

niech E2 będzie zdarzeniem uzyskania sumy 6.
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒ p (E2) = 5
zatem P(E2) = n (E2) / N(S) = 5/36
⇒ p (E2) = /P (E2) = (1 – 5/36)/(5/36) = 31/5.

5., Dwie kości, jedna niebieska i jedna pomarańczowa, są rzucane jednocześnie. Znajdź prawdopodobieństwo uzyskania

(i) równych liczb na obu

(ii) dwóch liczb pojawiających się na nich, których suma wynosi 9.,

rozwiązanie:

możliwe wyniki są

(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)

,

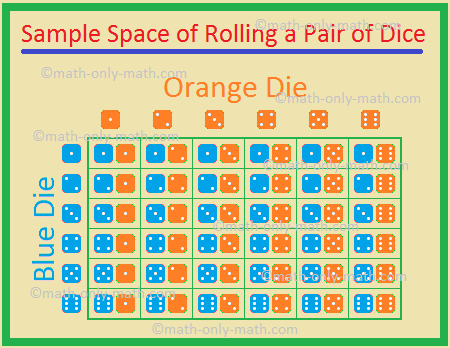
(i) liczba korzystnych wyników dla zdarzenia E

= liczba wyników o jednakowych liczbach na obu kościach

= 6 .

więc z definicji P (E) = \(\frac{6}{36}\)

= \(\frac{1}{6}\)

(ii) liczba pozytywnych wyników dla zdarzenia F

= Liczba wyników, w których dwie pojawiające się na nich liczby mają sumę 9

= 4 .

zatem z definicji P (F) = \(\frac{4}{36}\)

= \(\frac{1} {9}\).

te przykłady pomogą rozwiązać różne rodzaje problemów w oparciu o prawdopodobieństwo rzucania dwoma kośćmi.,p>Probability and Playing Cards

Probability for Rolling Two Dice

Solved Probability Problems

Probability for Rolling Three Dice

9th Grade Math

From Probability for Rolling Two Dice to HOME PAGE