div>

dziś przyjrzymy się najpopularniejszemu modelowi cen opcji. Model Blacka Scholesa, znany również jako metoda Blacka-Scholesa-Mertona, jest matematycznym modelem kontraktów opcyjnych. Jego działanie polega na oszacowaniu zmienności instrumentów finansowych. Technika opiera się na założeniu, że ceny podążają za rozkładem lognormalnym. Na tej podstawie uzyskuje wartość opcji.,

jest bardziej odpowiedni dla opcji niezależnych od ścieżki, których inwestorzy nie mogą wykonać przed terminem płatności. To sprawia, że różni się od dwumianowego modelu wyceny opcji, który jest neutralną pod względem ryzyka metodą wyceny opcji zależnych od ścieżki (np. opcje Amerykańskie).

analitycy i inwestorzy uważają Black Scholes za jedno z podstawowych pojęć współczesnej teorii finansowej.

wprowadzony w 1973 roku w Journal of Political Economy przez Fischera Blacka i Myrona Scholesa, a później zbudowany przez Roberta Mertona, model zdobył Nagrodę Nobla w dziedzinie ekonomii w 1997 roku.,

model wynika z równania różniczkowego, którego używamy do rozwiązania dla cen opcji. Używamy standardowej odmiany modelu dla opcji stylu Europejskiego. Black Scholes nie nadaje się do opcji W Stylu Amerykańskim, ponieważ nie uważa, że inwestorzy mogą skorzystać z tych opcji w dowolnym momencie przed ich datą wygaśnięcia.

metoda zakłada, że cena akcji bazowych ma rozkład lognormalny, ponieważ nie może być ujemna. Rozkład, na którym opiera się model, opiera się na ruchu Browna, teorii przewidywania naturalnie występujących zjawisk losowych.,

używamy tego modelu do obliczania szacunkowej ceny opcji, wykorzystując następujące informacje:

  • aktualna cena;
  • cena wykonania;
  • czas wygaśnięcia;
  • Oczekiwany zysk z dywidendy;
  • oczekiwana stopa procentowa; i
  • oczekiwana zmienność.

początkowo model nie uwzględnia efektu wypłaty dywidendy. W związku z tym często dostosowuje się go do tego, określając wartość dnia bez dywidendy aktywów bazowych., Zysk z dywidendy powoduje obniżenie aktualnej ceny akcji, ponieważ posiadacz opcji rezygnuje z dywidend.

założenia

model Blacka Scholesa działa tylko wtedy, gdy przyjmiemy pewne założenia.,

  • rynki są całkowicie wydajne, co oznacza, że nie możemy przewidzieć ich ruchów;
  • opcje kupna i sprzedaży nie wiążą się z kosztami transakcji;
  • zarówno zmienność aktywów bazowych, jak i stopa wolna od ryzyka pozostają na stałym poziomie do daty wygaśnięcia, co nie jest poprawne, ponieważ w rzeczywistości zmienność zmienia się wraz z podażą i popytem; i
  • zwrot z aktywów bazowych nie jest prawidłowy.podążaj za rozkładem normalnym.,

    • formuła Black Scholesa

    formuła modelu jest dość skomplikowana matematycznie, co nie jest szczególnym zagadnieniem, ponieważ możemy użyć specjalistycznych narzędzi do jego obliczenia. Ale nadal ważne jest, aby zrozumieć, jak to działa.,

    aby obliczyć cenę opcji call, w modelu Black Scholes, możemy użyć następującego równania:

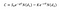
    gdzie:

    • S0 to cena akcji;
    • e to liczba wykładnicza;
    • Q to procent zysku z dywidendy;
    • t to termin (jeden rok to t=1, podczas gdy sześć miesięcy to T=0.,5);
    • N(d1) to delta opcji call, co oznacza zmianę ceny wywołania w stosunku do zmiany ceny akcji;
    • K to cena wykonania;
    • r to stopa wolna od ryzyka; i
    • N(d2) to prawdopodobieństwo, że przyszła cena akcji będzie wyższa niż cena wykonania, prawdopodobieństwo, że skorzystamy z tej opcji.

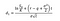
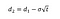
    jedna strona to cena akcji pomnożona przez skumulowany standardowy rozkład normalny d1, a druga — cena wykonania, zdyskontowana do czasu T, a następnie pomnożona przez skumulowany standardowy rozkład normalny d2., gdzie można obliczyć D1 i D2 według wzorów:

    gdzie σ jest zmiennością rentowności instrumentu bazowego.,

    możemy zastosować tę samą logikę dla opcji put:

    dołącz do naszego newslettera, aby uzyskać bezpłatny szablon analizy porównawczej Excel

    przykład obliczenia Black Scholes

    aby lepiej zilustrować koncepcję modelu Black Scholes, wykonamy następujące zadania: spójrz na poniższy model. Zaczynamy od wejścia modelu., Jak omówiono powyżej, potrzebujemy następujących sześciu zmiennych do obliczenia wartości opcji call I put.

    następnie obliczymy parametry opcji. Zaczynając od d1, otrzymujemy 0,39 z założeń modelu.

    aby go obliczyć, po prostu przenosimy wzór na D1 do Excela.,

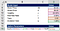
    Following the same approach, we calculate d2, N(d1) and N(d2).

    With those, we can calculate the Call Option Price and the Put Option Price.,

    możemy użyć reguły parzystości Call-Put, aby sprawdzić, czy nasze formuły i obliczenia są poprawne.

    teraz, gdy mamy nasz model do obliczania cen opcji call I put, możemy pójść o krok dalej i przyjrzeć się, w jaki sposób różne parametry wejściowe wpływają na wyniki naszego modelu., Funkcjonalność tabeli danych w programie Excel jest doskonałym narzędziem do przygotowania tabel analizy wrażliwości dla naszych zmiennych. W artykule poświęconym analizie wrażliwości dowiesz się, jak korzystać z tabel danych.

    przyjrzyjmy się cenie akcji, jeśli zmieni się ona z 10 euro na 100 euro i jak wpływa na wartości Call I Put. Zauważamy, że opcja Call nie ma żadnej wartości, dopóki cena akcji nie osiągnie 40 euro. Widzimy odwrotność dla opcji Put, gdzie jej wartość osiąga zero, gdy cena akcji wzrośnie powyżej 85 euro.,

    jeśli przygotujemy tę samą tabelę czułości dla ceny wykonania, możemy zaobserwować odwrotną zależność. Wraz ze wzrostem ceny wykonania, wartość wezwania spada, a wartość Put wzrasta.

    przyjrzyjmy się również kursowi bez ryzyka., Wraz ze wzrostem, Zwiększa to również wymaganą stopę zwrotu. Następnie zmniejsza to wartość zapasów. Zauważamy bezpośredni związek, ponieważ wzrasta stopa wolna od ryzyka, wzrasta również wartość opcji Call, podczas gdy wartość opcji Put zmniejsza swoją wartość.

    stosując to samo podejście, możesz przyjrzeć się pozostałym parametrom i ich wpływowi na wartości opcji., Możesz pobrać Model Excel na końcu artykułu i przejść do analizy wrażliwości w tam.

    przykładowy model można pobrać w Excelu w oryginalnym artykule.

    wnioski

    należy pamiętać, że model Blacka-Scholesa-Mertona jest pojęciem teoretycznym. Używamy go do próby oszacowania zachowania rynku. Jednak kiedy wykorzystujemy wyniki w naszym procesie decyzyjnym, musimy zrozumieć założenia leżące u podstaw modelu i to, w jaki sposób odbiega on od rzeczywistości.,

    formuła pomogła handlowi opcjami stać się bardziej popularnym, ponieważ sprawia, że wygląda mniej jak hazard. Obecnie różne modyfikacje Black Scholes są powszechnie popularne jako podstawowe strategie kontroli ryzyka, związane z zmiennością.

    możesz okazać swoje wsparcie, dzieląc się artykułem ze współpracownikami i przyjaciółmi.