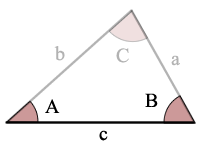
Triangle Figure Angle-Side-Angle (Asa)
A = angle a
B = angle C
a = side a
b = side b
C = side C
p = perimeter
s = semi-perimeter
K = obszar
r = promień okręgu wpisanego
R = promień okręgu określonego
kalkulator użyj
każda opcja obliczeń, pokazana poniżej, ma podpunkty, które wymieniają sekwencję metod używanych w tym kalkulatorze do rozwiązania dla nieznanego kąta i wartości bocznych, w tym sumy kątów w trójkącie, prawo sinusów i prawo cosinusów., Nie są to jedyne sekwencje, których można użyć do rozwiązania tego typu problemów.
- Zobacz również te kalkulatory trygonometryczne:
- Kalkulator prawa cosinusów
- Kalkulator prawa sinusów
rozwiązywanie twierdzeń trójkąta
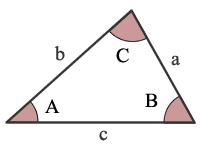
AAA to Kąt, Kąt, Kąt
określenie trzech kątów trójkąta nie jednoznacznie identyfikuje jednego trójkąta. Dlatego określenie dwóch kątów tringla pozwala obliczyć tylko trzeci kąt.,
biorąc pod uwagę rozmiary 2 kątów trójkąta można obliczyć rozmiar trzeciego kąta. Suma będzie równa 180° lub π radianów.
C = 180° – A – B (w stopniach)
c = π – a – b (w radianach)
AAS to Kąt, Kąt, bok
biorąc pod uwagę rozmiar 2 kątów i 1 strony naprzeciwko jednego z podanych kątów, można obliczyć rozmiary pozostałych 1 kątów i 2 boków.
użyj reguły Sumy kątów, aby znaleźć inny kąt, a następnie
użyj prawa sinusów, aby rozwiązać dla każdej z pozostałych dwóch stron.,
ASA to kąt, bok, kąt
biorąc pod uwagę rozmiar 2 kątów i rozmiar boku, który znajduje się pomiędzy tymi 2 kątami, można obliczyć rozmiary pozostałych 1 kątów i 2 boków.
użyj reguły Sumy kątów, aby znaleźć inny kąt, a następnie
użyj prawa sinusów, aby rozwiązać dla każdej z pozostałych dwóch stron.,
ASS (lub SSA) to kąt, Bok, Bok
biorąc pod uwagę rozmiar 2 stron (a i C, gdzie a< c) i rozmiar kąta A, który nie znajduje się pomiędzy tymi 2 stronami, możesz być w stanie obliczyć rozmiary pozostałych 1 stron i 2 kątów, w zależności od następujących warunków.,F Cosines do rozwiązania dla każdego z pozostałych dwóch kątów
prezentują 2 pełne rozwiązania
przykład: 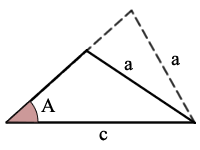
sin(A) = A/c, istnieje jeden możliwy Trójkąt
użyj prawa sinusów, aby rozwiązać dla kąta, C
użyj reguły Sumy kątów, aby znaleźć inny kąt, Bp
użyj prawa sinusów, aby rozwiązać ostatnią stronę, b
przykład: 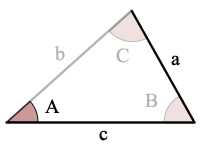
sin(a) >a/c, nie ma możliwych trójkątów
uwaga o błędzie: sin(a) >A/C więc nie ma rozwiązań i nie ma trójkąta!,
przykład: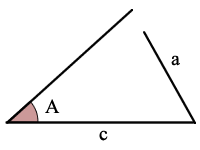
SAS to Side, Angle, Side
biorąc pod uwagę rozmiar 2 boków (c i a) oraz Rozmiar kąta B, który znajduje się pomiędzy tymi 2 bokami, można obliczyć rozmiary pozostałych 1 boków i 2 kątów.
użyj prawa cosinusów, aby rozwiązać dla pozostałej strony, b
określ, która strona, a lub c, jest najmniejsza i użyj prawa sinusów, aby rozwiązać dla wielkości przeciwległego kąta, odpowiednio A lub C.,
użyj reguły Sumy kątów, aby znaleźć ostatni kąt
SSS to Side, Side, Side
biorąc pod uwagę rozmiary 3 boków, możesz obliczyć rozmiary wszystkich 3 kątów w trójkącie.
użyj prawa cosinusów do rozwiązania dla kątów. Możesz również użyć reguły Sumy kątów, aby znaleźć ostateczny kąt, gdy znasz 2 z nich.,sin – 1
prawo Cosines
Jeśli A, b I c są długościami nóg trójkąta przeciwnego odpowiednio do kątów a, b i C; wtedy prawo cosines stwierdza:
A2 = c2 + b2 – 2BC cos a, rozwiązywanie dla cos A, cos A = ( b2 + c2 – A2 ) / 2BC
B2 = A2 + c2 – 2CA cos B, rozwiązywanie dla cos B, cos B = ( C2 + A2 – B2 ) / 2CA
C2 = B2 + A2 – 2AB Cos C, rozwiązywanie dla Cos C, Cos C = ( a2 + b2 – c2 ) / 2AB
rozwiązywanie, na przykład, dla kąta, a = cos-1
inne cechy trójkąta
obwód trójkąta, p = a + b + c
półokrąg trójkąta, s = 0.,5 * (a + b + c)
obszar trójkąta, k = √
promień okręgu wpisanego w trójkąt, r = √
promień okręgu opisanego w trójkącie, r = (abc) / (4K)
Referencje/ Czytaj dalej
Weisstein, Eric W. „twierdzenie ASSA.”Z MathWorld-Zasobów Internetowych Wolframa. Twierdzenie o dupach.
Matematyka to zabawa-rozwiązywanie trójkątów SAS
















Dodaj komentarz