Gdy kąty trójkąta nie sumują się do 180 stopni

1. Wprowadzenie

czy kąty trójkąta sumują się do 180 stopni czy $\pi$ radianów? Odpowiedź brzmi: „czasami tak, czasami nie”. Czy to ważne pytanie? Tak, ponieważ prowadzi to do zrozumienia, że istnieją różne geometrie oparte na różnych aksjomatach lub „regułach gry w geometrię”. Czy to sensowne pytanie? Cóż, przynajmniej nie dopóki nie uzgodnimy znaczenia słów ” kąt ” i „kąt”, nie dopóki nie poznamy zasad gry., W tym artykule pokrótce omówimy podstawowe aksjomaty i przedstawimy prosty dowód, że suma kątów trójkąta na powierzchni sfery jednostkowej nie jest równa $ \ pi$, ale $ \ pi $ plus powierzchnia trójkąta. Użyjemy faktu, że powierzchnia powierzchni kuli Jednostkowej wynosi $4\pi$.

2. Wielkie twierdzenie

zanim będziemy mogli powiedzieć, czym jest trójkąt, musimy uzgodnić, co rozumiemy przez punkty i linie. Pracujemy nad geometrią sferyczną (dosłownie geometrią na powierzchni kuli)., W tej geometrii przestrzeń jest powierzchnią kuli; punkty są punktami na tej powierzchni, a linia najkrótszej odległości między dwoma punktami jest wielkim okręgiem zawierającym te dwa punkty. Wielki okrąg (jak równik) rozcina sferę na dwie równe półkule. Geometria ta ma oczywiste zastosowanie do odległości między miejscami i dróg powietrznych na Ziemi.,

obracająca się kula pokazująca Wielki okrąg

kąt między dwoma wielkimi okręgami w punkcie P jest kątem Euklidesowym między kierunkami okręgów (lub ściśle między stycznymi do okręgów w punkcie P). Nie stwarza to trudności w nawigacji po ziemi, ponieważ w danym punkcie myślimy o kącie między dwoma kierunkami tak, jakby ziemia była płaska w tym punkcie.

Luna to część powierzchni kuli ograniczona przez dwa wielkie okręgi, które spotykają się w punktach antypodowych., Najpierw rozważamy obszar Luny, a następnie wprowadzamy kolejny wielki okrąg, który dzieli Lunę na Trójkąty.

obrotowa kula pokazująca 4 lunes

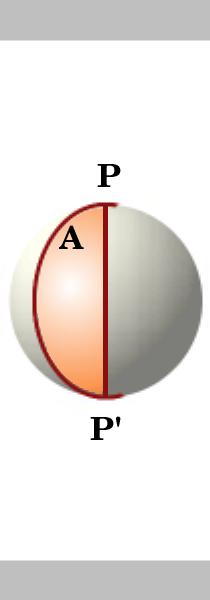
Lemma.

pole Luny na okręgu o promieniu jednostkowym jest dwa razy większe od jego kąta, czyli jeśli kąt Luny jest A, to jego pole wynosi 2A. dwa wielkie okręgi przecinające się w punktach antypodowych P I P' dzielą sferę na 4 Luny. Powierzchnia powierzchni kuli Jednostkowej wynosi $4\pi$.,

obszary lunes są proporcjonalne do ich kątów w P więc obszar Lunes z kątem a jest

${\frac{a}{2\pi}\times {4\pi}= {2A}}$

Ćwiczenie 1.

Jakie są obszary pozostałych 3 lunes? Czy twoje 4 obszary sumują się do $ 4 \ pi$?

Sprawdź odpowiedzi tutaj .

boki trójkąta ABC to segmenty trzech wielkich okręgów, które w rzeczywistości przecinają powierzchnię kuli na osiem trójkątów sferycznych. Pomiędzy dwoma wielkimi kręgami przez punkt A znajdują się cztery kąty., Oznaczamy kąt wewnątrz trójkąta ABC jako kąt A, a pozostałe kąty trójkąta ABC jako kąt B i kąt C.

obracająca się kula pokazuje 8 trójkątów

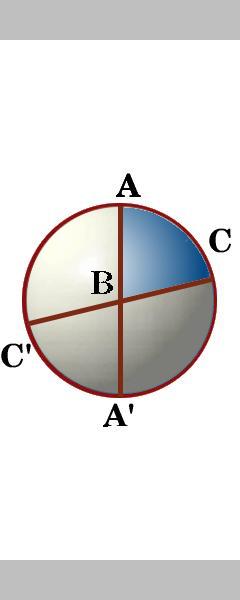
Ćwiczenie 2

obracająca się kula czy możesz nazwać osiem trójkątów i powiedzieć, czy któryś z nich ma ten sam obszar? Sprawdź odpowiedzi tutaj .

rozważmy Trójkąt sferyczny ABC na kuli jednostkowej o kątach A, B i C. wówczas pole trójkąta ABC wynosi

A + B + C – $\pi$.,

na diagramie przedstawiono widok z perspektywy półkuli, który ma linię przez AC jako granicę. Obszary oznaczone Area 1 i Area 3 to lunety o kątach odpowiednio A i C. Rozważmy lunes przez B i B'. Trójkąt ABC jest przystający do trójkąta A ' B 'C', więc muszka w kształcie cieniowanego obszaru, oznaczonego obszarem 2, który jest sumą obszarów trójkątów ABC i A’BC', jest równa powierzchni Luny o kącie B, który jest równy 2B.,

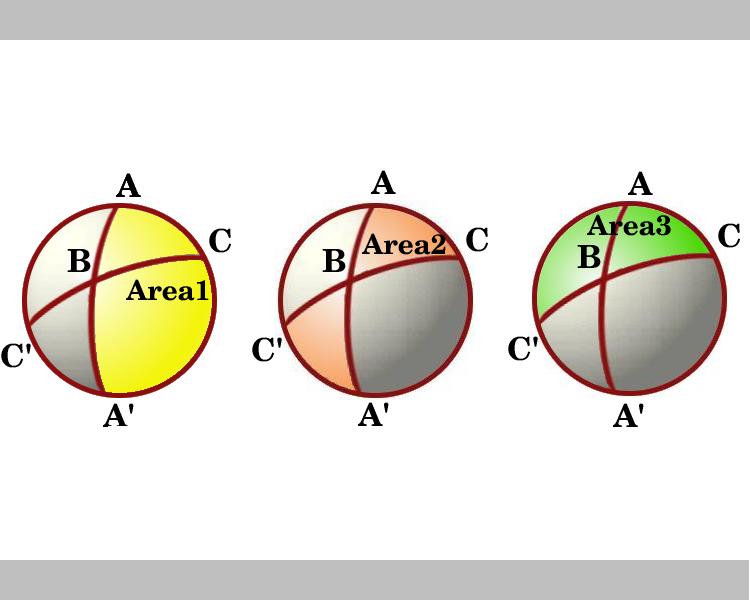
Tak więc na diagramie widzimy obszary trzech lunes i, używając lematu, są to:

Area 1 = 2A
Area 2 = 2B
Area 3 = 2C

sumując te trzy obszary uwzględniamy obszar trójkąta ABC trzy razy., Hence

3., Nie-euklidesowa Geometria

czasami rewolucyjne odkrycia to nic innego, jak rzeczywiście zobaczyć to, co było pod naszym nosem przez cały czas. Tak było w przypadku odkrycia geometrii nieeuklidesowej w XIX wieku. Przez około 2000 lat po tym, jak Euklid napisał swoje „elementy” w 325 r. p. n. e., ludzie próbowali udowodnić postulat równoległy jako twierdzenie w geometrii z innych aksjomatów, ale zawsze nie powiodło się i to jest długa historia., Tymczasem matematycy przez cały czas używali geometrii sferycznej, geometrii, która jest zgodna z innymi aksjomatami geometrii euklidesowej i zawiera wiele takich samych twierdzeń, ale w których postulat równoległości nie mieści się. Przez cały czas mieli pod nosem przykład nie-euklidesowej geometrii.

pomyśl o linii L i Punkcie P nie NA L. Duże pytanie brzmi: „ile linii można narysować przez P równolegle do L?”W geometrii euklidesowej odpowiedź brzmi” dokładnie jedna ” i jest to jedna z wersji postulatu równoległego., Jeśli suma kątów każdego trójkąta w geometrii wynosi $ \ pi$ radianów, to postulat równoległy posiada i odwrotnie, te dwie własności są równoważne.

w geometrii sferycznej podstawowe aksjomaty, które zakładamy (zasady gry), różnią się od geometrii euklidesowej – jest to geometria nieeuklidesowa. Zauważyliśmy, że w geometrii sferycznej kąty trójkątów nie zawsze sumują się do$ \ pi $ radianów, więc nie spodziewalibyśmy się, że postulat równoległości się utrzyma., W geometrii sferycznej linie proste (linie najkrótszej odległości lub geodezyjne)są wielkimi kołami, a każda linia w geometrii przecina co drugą linię w dwóch punktach. Odpowiedź na duże pytanie o równoległości brzmi: „jeśli mamy linię L i punkt P nie na L, to nie ma linii przez P równoległych do linii L.,”

greccy matematycy (na przykład Ptolemeusz c 150) obliczyli pomiary trójkątów sferycznych pod kątem prostym i pracowali ze wzorami trygonometrii sferycznej, a arabscy matematycy (na przykład Jabir ibn Aflah c 1125 i Nasir ed-din c 1250) rozszerzyli pracę jeszcze bardziej. Formuła omawiana w tym artykule została odkryta przez Harriota w 1603 roku i opublikowana przez Girarda w 1629 roku. Dalsze prace nad tą tematyką rozwinął Saccerhi (1667-1733).,

wszystko to zostało w dużej mierze niezauważone przez XIX-wiecznych odkrywców geometrii hiperbolicznej, która jest kolejną geometrią Nieeuklidesową, w której postulat równoległości nie trzyma się. W geometrii sferycznej (zwanej również geometrią eliptyczną) kąty trójkątów sumują się do więcej niż $\pi$ radianów, a w geometrii hiperbolicznej kąty trójkątów sumują się do mniej niż $ \ pi$ radianów.

Więcej informacji znajdziesz w artykule Alana Beardona ” ile jest geometrii?”oraz artykuł Keitha Carne „dziwne Geometrie”., Istnieje kilka praktycznych zajęć, które możesz wypróbować, aby zbadać te geometrie dalej, można znaleźć na http://nrich.maths.org/MOTIVATE/conf8/index.html