mężczyzn. Czuję, że podoba mi się to, co mówisz.
Soc . A ja, Meno, podoba mi się to, co mówię.
z Meno Platona
długość przekątnej kwadratu jednostki jest równa pierwiastkowi kwadratowemu z 2.
długość przekątnej kwadratu jednostki jest równa √2. To nie jest dobra wiadomość. Każdy, kto kiedykolwiek zetknął się z twierdzeniem Pitagorasa, jest tego świadomy., W trójkącie prostokątnym równoramiennym z nogami o długości 1, przeciwprostokątna, zgodnie z twierdzeniem Pitagorasa – 12 + 12 = (przeciwprostokątna)2-jest rzeczywiście długości √2. Motywacją dla tej strony jest nie tyle sam fakt, co sposób pokazania go bez odwoływania się do słynnego twierdzenia. Rzeczywiście, można by argumentować, że twierdzenie Pitagorasa mogło być nadużywane, zobacz ciekawy przykład.
argument, który sięga do postaci narysowanej przez Sokratesa w Meno Platona, mógł być znany samemu Pitagorasowi, chociaż ten ostatni żył sto lat wcześniej.,
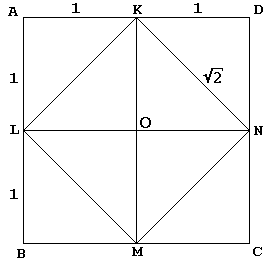
w oknie dialogowym Sokrates, w swój zwykły sposób, prowadzi młodego niewolnika do budowy kwadratu dwukrotnie większego od danego:
dany kwadrat KLMN z Centrum O jest najpierw pocięty przez jego przekątne na 4 równe trójkąty. Sokrates osadza KLMN w większym kwadracie ABCD, jakby odzwierciedlał te trójkąty w swojej przeciwprostokątnej. Niewolnik następnie przyznaje – a kto by nie chciał? – ten kwadrat ABCD jest dwa razy większy od kwadratu KLMN.
prawdę mówiąc, Plac Sokratesa ABCD mierzył 4 z boku, tak że plac KLMN miał powierzchnię 8., Jest oczywiste, że gdy zaczniemy od kwadratu ABCD z boku 2 (a więc z obszaru 4), kwadratowy KLMN będzie miał powierzchnię 2.
obecnie, ogólnie rzecz biorąc, dla liczby dodatniej A, √A definiuje się jako liczbę, której kwadratem jest A:
(√a)2.
z drugiej strony, każdy uczeń obszarów wie, że pole kwadratu o boku b jest równe B2. Wynika z tego, że bok kwadratu o polu a jest dokładnie √A. wnioskujemy, że bok kwadratu KLMN jest równy √2. Po pierwsze,
KN = √A.
centralnym punktem argumentu jest fakt, że na diagramie KN odgrywa podwójną rolę., Oprócz tego, że jest jednym z boków kwadratowego KLMN, służy również jako przekątna kwadratowego OKDN. Ten ostatni jest oczywiście kwadratem jednostkowym, co dowodzi naszego twierdzenia.
(z nieco innej perspektywy ten sam epizod jest wspominany gdzie indziej.)
















Dodaj komentarz