Show Mobile Notice Show All Notes Hide All Notes
sekcja 3-1: równania parametryczne i krzywe
do tego momentu (zarówno w rachunku I, jak i rachunku II) przyjrzeliśmy się prawie wyłącznie funkcjom w postaci \(y = f\left (x \right)\) lub \ (x = h \ left (y \right)\) i prawie wszystkie formuły, które opracowaliśmy, wymagają, aby funkcje były w jednej z tych dwóch form. Problem polega na tym, że nie wszystkie krzywe lub równania, na które chcielibyśmy spojrzeć, łatwo wpadają w tę formę.
Weźmy na przykład okrąg. Łatwo jest zapisać równanie okręgu wyśrodkowanego na początku o promieniu \(r\).,
\
jednak nigdy nie będziemy w stanie zapisać równania okręgu w dół jako pojedynczego równania w żadnej z powyższych form. Oczywiście możemy rozwiązać dla \(x\) lub \(y\), ponieważ następujące dwie formuły pokazują
\
, ale w rzeczywistości są dwie funkcje w każdej z nich. Każda formuła daje część okręgu.
\
Niestety, zwykle pracujemy nad całym kręgiem, lub po prostu nie możemy powiedzieć, że będziemy pracować tylko nad jedną jego częścią. Nawet jeśli możemy zawęzić sprawy do tylko jednej z tych części, funkcja jest nadal często dość nieprzyjemna w pracy.,
\
ta trzecia zmienna jest zwykle oznaczana przez \(t\) (Jak to zrobiliśmy tutaj), ale nie musi być oczywiście. Czasami będziemy ograniczać wartości \(t\), które będziemy używać, a w innych czasach nie będziemy. to często będzie zależeć od problemu i tylko to, co staramy się zrobić.
aby pomóc wizualizować, co to jest krzywa parametryczna udawaj, że mamy duży zbiornik wody, który jest w ciągłym ruchu i upuszczamy piłkę ping-ponga do zbiornika., Punkt \(\left ({x,y} \right) = \ left ({f \ left (t \right), g\left( t \right)} \ right)\) będzie wtedy reprezentować położenie piłki do ping ponga w zbiorniku w czasie \(t\), a krzywa parametryczna będzie śladem wszystkich lokalizacji piłki do ping ponga. Zauważ, że nie zawsze jest to poprawna analogia, ale na początku przydatne jest wizualizowanie, czym jest krzywa parametryczna.
Szkicowanie krzywej parametrycznej nie zawsze jest łatwe. Spójrzmy na przykład, aby zobaczyć jeden ze sposobów szkicowania krzywej parametrycznej., Ten przykład zilustruje również, dlaczego ta metoda zwykle nie jest najlepsza.
w tym momencie naszą jedyną opcją do szkicowania krzywej parametrycznej jest wybranie wartości \(t\), podłączenie ich do równań parametrycznych, a następnie wykreśl punkty. Więc podłączmy niektóre \(t\) ' s.,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Niestety w tej chwili nie ma prawdziwej odpowiedzi na to pytanie. Po prostu wybieramy \(t\) ' S, dopóki nie będziemy dość pewni, że mamy dobry pomysł na to, jak wygląda krzywa. To właśnie ten problem ze zbieraniem „dobrych” wartości \(t\) sprawia, że ta metoda szkicowania krzywych parametrycznych jest jedną z gorszych opcji. Czasami nie mamy wyboru, ale jeśli mamy wybór, powinniśmy go unikać.
w późniejszych przykładach omówimy alternatywną metodę Wykresów, która pomoże wyjaśnić, w jaki sposób wybrano te wartości \(t\).,
mamy jeszcze jeden pomysł do omówienia, zanim rzeczywiście szkicujemy krzywą. Krzywe parametryczne mają kierunek ruchu. Kierunek ruchu jest określony przez zwiększenie \(t\). Tak więc, podczas kreślenia krzywych parametrycznych, dołączamy również strzałki, które pokazują kierunek ruchu. Często podajemy wartość \(t\), która dała określone punkty na wykresie, a także wyjaśniamy wartość \(t\), która dała ten konkretny punkt.
oto szkic tej krzywej parametrycznej.
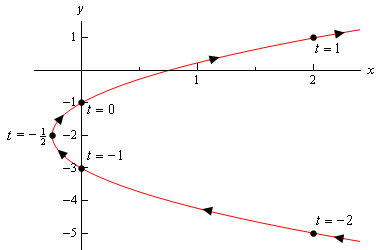
więc wygląda na to, że mamy parabolę, która otwiera się po prawej stronie.,
zanim zakończymy ten przykład, jest nieco ważny i subtelny punkt, który musimy najpierw omówić. Zauważ, że upewniliśmy się, że umieściliśmy część szkicu po prawej stronie punktów odpowiadających \(t = – 2\) i \(T = 1\), aby wskazać, że są tam części szkicu. Gdybyśmy po prostu zatrzymali szkic w tych punktach, wskazujemy, że nie było żadnej części krzywej po prawej stronie tych punktów i wyraźnie będzie. Po prostu nie obliczyliśmy żadnego z tych punktów.,
może się to wydawać nieistotnym punktem, ale jak zobaczymy w następnym przykładzie, jest to ważniejsze niż mogłoby nam się wydawać.
zanim zajmiemy się znacznie łatwiejszym sposobem szkicowania tego wykresu, zajmijmy się najpierw kwestią limitów dla parametru. W poprzednim przykładzie nie mieliśmy żadnych ograniczeń co do parametru. Bez ograniczeń parametru wykres będzie kontynuowany w obu kierunkach, jak pokazano na powyższym szkicu.
często jednak będziemy mieli ograniczenia dotyczące parametru, co wpłynie na szkic równań parametrycznych., Aby zobaczyć ten efekt, spójrzmy na lekką odmianę poprzedniego przykładu.
zauważ, że jedyną różnicą jest tutaj obecność limitów na \(t\). Wszystkie te limity mówią nam, że nie możemy przyjąć żadnej wartości \(t\) poza tym zakresem. Dlatego krzywa parametryczna będzie tylko częścią powyższej krzywej. Oto krzywa parametryczna dla tego przykładu.,
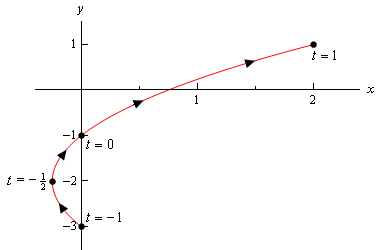
zauważ, że w tym szkicu rozpoczęliśmy i zatrzymaliśmy szkic bezpośrednio na punktach pochodzących z punktów końcowych zakresu \(t\)’s. Porównaj to ze szkicem w poprzednim przykładzie, gdzie mieliśmy część szkicu po prawej stronie punktów „początek” i „koniec”, które obliczyliśmy.
w tym przypadku krzywa zaczyna się od \(t = – 1\) i kończy się na \(t = 1\), podczas gdy w poprzednim przykładzie krzywa tak naprawdę nie zaczynała się od prawej większości punktów, które obliczyliśmy., Musimy być jasne w naszych szkicach, jeśli krzywa zaczyna / kończy się dokładnie w punkcie, lub jeśli ten punkt był po prostu pierwszy / ostatni, który obliczyliśmy.
nadszedł czas, aby przyjrzeć się prostszej metodzie szkicowania tej parametrycznej krzywej. Metoda ta wykorzystuje fakt, że w wielu, ale nie wszystkich, przypadkach możemy faktycznie wyeliminować parametr z równań parametrycznych i uzyskać funkcję obejmującą tylko \(x\) i \(y\). Czasami nazywamy to równaniem algebraicznym, aby odróżnić je od oryginalnych równań parametrycznych., Będą dwa małe problemy z tą metodą, ale łatwo będzie rozwiązać te problemy. Należy jednak pamiętać, że nie zawsze będziemy w stanie to zrobić.
to, jak wyeliminujemy parametr, będzie zależeć od równań parametrycznych, które mamy. Zobaczmy, jak wyeliminować parametr dla zbioru równań parametrycznych, nad którymi pracowaliśmy do tego momentu.
uzyskanie szkicu krzywej parametrycznej po wyeliminowaniu parametru wydaje się dość proste. Wszystko, co musimy zrobić, to wykreślić równanie, które znaleźliśmy, eliminując parametr., Jak już wspomniano, istnieją dwa małe problemy z tą metodą. Pierwszym jest kierunek ruchu. Równanie obejmujące tylko \(x\) i \(y\) nie da kierunku ruchu krzywej parametrycznej. Jest to jednak na ogół łatwy problem do naprawienia. Rzućmy okiem na pochodne równań parametrycznych z ostatniego przykładu. Są one,
\
zauważ, że pochodna \ (x\) nie jest tak użyteczna dla tej analizy, ponieważ będzie zarówno dodatnia, jak i ujemna, a zatem \(x\) będzie zarówno wzrastać, jak i zmniejszać się w zależności od wartości \(t\)., To nie pomaga w kierunku, ponieważ podążanie za krzywą w obu kierunkach będzie wykazywało zarówno rosnącą, jak i malejącą \(x\).
w niektórych przypadkach tylko jedno z równań, takie jak ten przykład, da kierunek, podczas gdy w innych przypadkach można użyć jednego z nich. Możliwe jest również, że w niektórych przypadkach oba pochodne byłyby potrzebne do określenia kierunku. Zawsze będzie zależeć od indywidualnego zbioru równań parametrycznych.,
drugi problem z wyeliminowaniem parametru jest najlepiej zilustrowany w przykładzie, ponieważ w pozostałych przykładach napotkamy ten problem.
ok, to był naprawdę długi przykład. Większość tego typu problemów nie jest tak długa. Po prostu mieliśmy wiele do omówienia w tym jednym, więc mogliśmy uzyskać kilka ważnych pomysłów z drogi. Pozostałe przykłady w tej sekcji nie powinny trwać tak długo.
przyjrzyjmy się teraz innemu przykładowi, który zilustruje ważną ideę dotyczącą równań parametrycznych.,
tak więc w dwóch ostatnich przykładach widzieliśmy dwa zestawy równań parametrycznych, które w jakiś sposób dały ten sam wykres. Jednak, ponieważ wyśledzili Wykres różną liczbę razy, naprawdę musimy myśleć o nich jako o różnych krzywych parametrycznych przynajmniej w jakiś sposób. Może się to wydawać różnicą, o którą nie musimy się martwić, ale jak zobaczymy w późniejszych sekcjach, może to być bardzo ważna różnica. W niektórych późniejszych sekcjach będziemy potrzebować krzywej, która zostanie wyśledzona dokładnie raz.,
zanim przejdziemy do innych problemów, krótko przyjrzyjmy się, co się dzieje, zmieniając \(t\) na nt w tego rodzaju równaniach parametrycznych. Gdy mamy do czynienia z równaniami parametrycznymi obejmującymi tylko sinusy i cosiny i oba mają ten sam argument, jeśli zmienimy argument z \(t\) na nt, po prostu zmienimy prędkość, z jaką krzywa jest śledzona. Jeśli \(n > 1\) zwiększymy prędkość, a jeśli \(N < 1\) zmniejszymy prędkość.
przyjrzyjmy się jeszcze kilku przykładom.,
do tego momentu widzieliśmy przykłady, które prześledziłyby kompletny wykres, który otrzymaliśmy, eliminując parametr, jeśli weźmiemy wystarczająco duży zakres \(t\) ' S. jednak w poprzednim przykładzie widzieliśmy, że nie zawsze tak będzie. Jest więcej niż możliwe, aby mieć zestaw równań parametrycznych, które będą stale śledzić tylko część krzywej. Zazwyczaj możemy określić, czy tak się stanie, szukając limitów na \(x\) i \ (y\), które są nam narzucone przez równanie parametryczne.,
często będziemy używać równań parametrycznych do opisu ścieżki obiektu lub cząstki. Spójrzmy na przykład.
w tym momencie powinniśmy dać małe ostrzeżenie. Ze względu na związane z nimi pomysły skupiliśmy się na krzywych parametrycznych, które powtarzały fragmenty krzywej więcej niż jeden raz. Nie daj się jednak zbytnio zakorzenić w przekonaniu, że zawsze tak będzie. Wiele, jeśli nie Większość krzywych parametrycznych zostanie prześledzonych tylko raz. Pierwszy z nich jest tego dobrym przykładem. Krzywa parametryczna nigdy się nie powtórzy.,
jest jeszcze jeden ostatni temat do omówienia w tej sekcji, zanim przejdziemy dalej. Do tej pory zaczęliśmy od równań parametrycznych i wyeliminowaliśmy parametr do wyznaczenia krzywej parametrycznej.
są jednak chwile, w których chcemy iść w drugą stronę. Biorąc pod uwagę funkcję lub równanie, możemy zapisać dla niej zbiór równań parametrycznych. W takich przypadkach mówimy, że parametryzujemy funkcję.
jeśli weźmiemy przykłady 4 i 5 jako przykłady, możemy to zrobić dla elips (a więc okręgów)., Biorąc pod uwagę elipsę
\
zestaw równań parametrycznych dla niej będzie,
\
Ten zestaw równań parametrycznych będzie śledził elipsę zaczynając od punktu \(\left( {a,0} \right)\) i będzie śledził w kierunku przeciwnym do ruchu wskazówek zegara i będzie śledził dokładnie raz w zakresie \(0 \le t \le 2\pi \). Jest to dość ważny zestaw równań parametrycznych, ponieważ używany stale w niektórych przedmiotach z radzeniem sobie z elipsami i / lub kręgami.
każda krzywa może być parametryzowana w więcej niż jeden sposób. Każda z poniższych opcji będzie również parametryzować tę samą elipsę.,
\
obecność \ (\omega\) zmieni prędkość obrotu elipsy, jak widzieliśmy w przykładzie 5. Zauważ również, że dwa ostatnie będą śledzić elipsy zgodnie z ruchem wskazówek zegara (możesz to sprawdzić). Zauważ również, że nie wszystkie zaczną się w tym samym miejscu (jeśli pomyślimy o \(t = 0\) jako punkcie początkowym).
istnieje o wiele więcej parametryzacji elipsy oczywiście, ale masz pomysł. Ważne jest, aby pamiętać, że każda parametryzacja będzie śledzić krzywą raz z potencjalnie innym zakresem \(t\) ' s., Każda parametryzacja może obracać się z różnymi kierunkami ruchu i może zaczynać się w różnych punktach.
może się okazać, że potrzebujesz parametryzacji elipsy, która zaczyna się w określonym miejscu i ma określony kierunek ruchu, więc teraz wiesz, że dzięki pewnej pracy możesz zapisać zestaw równań parametrycznych, które dadzą ci zachowanie, którego szukasz.
teraz zapiszmy kilka innych ważnych parametryzacji i wszystkie komentarze dotyczące kierunku ruchu, punktu początkowego i zakresu \(t\) dla jednego śladu (jeśli dotyczy) są nadal prawdziwe.,
Po pierwsze, ponieważ okrąg jest niczym więcej niż szczególnym przypadkiem elipsy, możemy użyć parametryzacji elipsy, aby uzyskać równania parametryczne dla okręgu wyśrodkowanego na początku promienia \(r\). Jednym z możliwych sposobów parametryzacji okręgu jest
\
w tym momencie może się wydawać, że parametryzacja funkcji takiej jak ta nie jest zbyt przydatna, ale jest wiele przypadków, w których praca z parametryzacją zamiast samej funkcji będzie łatwiejsza lub może być nawet wymagana., Niestety, prawie wszystkie te przypadki występują w kursie Calculus III.
















Dodaj komentarz