Show Mobile Notice Show All Notes Hide All Notes
sekcja 4-11 : przybliżenia liniowe
w tej sekcji przyjrzymy się zastosowaniu nie pochodnych, ale linii stycznej do funkcji. Oczywiście, aby uzyskać linię styczną musimy wziąć pochodne, więc w pewien sposób jest to również zastosowanie pochodnych.
\
spójrz na poniższy wykres funkcji i jej linii stycznej.
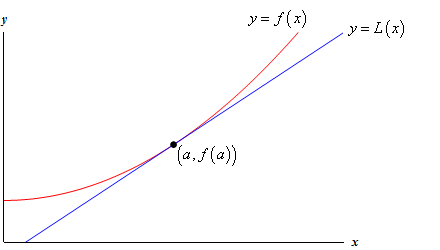
dlaczego mielibyśmy to zrobić? Spójrzmy na przykład.,
przybliżenia liniowe wykonują bardzo dobrą pracę przybliżania wartości \(f\left( x \right)\) tak długo, jak pozostajemy „blisko” \(x = a\). Jednak im dalej od \(x = a\) otrzymujemy gorsze przybliżenie. Głównym problemem jest to, że jak blisko musimy pozostać do \(x = a\), aby uzyskać dobre przybliżenie, zależy zarówno od funkcji, której używamy, jak i wartości \(x = a\), której używamy. Ponadto często nie będzie łatwego sposobu przewidywania, jak daleko od \(x = a\) możemy się dostać i nadal mieć „dobre” przybliżenie.,
przyjrzyjmy się innemu przykładowi, który w niektórych miejscach jest dość mocno wykorzystywany.
jest to właściwie dość ważne przybliżenie liniowe. W optyce to przybliżenie liniowe jest często używane do uproszczenia formuł. To przybliżenie liniowe jest również używane do opisu ruchu wahadła i drgań w łańcuchu.
















Dodaj komentarz