korzenie wielomianu

pierwiastek lub zero funkcji jest liczbą, która po podłączeniu do zmiennej sprawia, że funkcja jest równa zeru. Tak więc pierwiastki wielomianu P (x) są wartościami x takimi, że P (x) = 0.

twierdzenie o Zerach racjonalnych

twierdzenie o Zerach racjonalnych stwierdza:

możemy użyć twierdzenia o Zerach racjonalnych, aby znaleźć wszystkie racjonalne zera wielomianu., Oto kroki:

  1. ułóż wielomian w porządku malejącym
  2. Zapisz wszystkie czynniki stałego terminu. Są to wszystkie możliwe wartości P.
  3. Zapisz wszystkie czynniki współczynnika wiodącego. Są to wszystkie możliwe wartości q.
  4. Zapisz wszystkie możliwe wartości. Pamiętaj, że ponieważ czynniki mogą być ujemne, I – muszą być uwzględnione oba te czynniki. Uprość każdą wartość i przekreśl wszystkie duplikaty.,
  5. użyj podziału syntetycznego do określenia wartości dla których P() = 0. Są to wszystkie racjonalne korzenie P (x).

przykład: Znajdź wszystkie racjonalne zera P(x) = x3-9x + 9 + 2×4-19×2.

rysunek %: podział syntetyczny

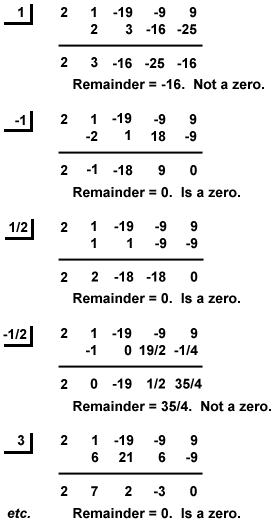
zatem racjonalne korzenie P(x) to x = – 3, -1, 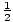, oraz 3.

często możemy użyć racjonalnego twierdzenia o Zerach do czynnika wielomianu., Używając podziału syntetycznego, możemy znaleźć jeden rzeczywisty korzeń a i możemy znaleźć iloraz, gdy P (x) jest dzielone przez x-a. następnie możemy użyć podziału syntetycznego, aby znaleźć jeden czynnik ilorazu. Możemy kontynuować ten proces, dopóki wielomian nie zostanie całkowicie uwzględniony.