Wanneer de hoeken van een driehoek niet optellen tot 180 graden

1. Inleiding

tellen de hoeken van een driehoek samen tot 180 graden of$ \ pi $ radialen? Het antwoord is ‘soms ja, soms Nee’. Is dit een belangrijke vraag? Ja, omdat het leidt tot een begrip dat er verschillende geometrieën zijn gebaseerd op verschillende axioma ’s of’regels van het spel van de meetkunde’. Is het een zinvolle vraag? Nou Nee, tenminste niet totdat we het eens zijn over de Betekenis van de woorden ‘angle’ en’ Triangle’, niet totdat we de regels van het spel kennen., In dit artikel bespreken we kort de onderliggende axioma ‘ s en geven een eenvoudig bewijs dat de som van de hoeken van een driehoek op het oppervlak van een eenheidsbol niet gelijk is aan $\pi$ maar aan $\pi$ plus de oppervlakte van de driehoek. We zullen het feit gebruiken dat de oppervlakte van het oppervlak van een eenheidsbol $4\pi$is.

2. De grote stelling

voordat we kunnen zeggen wat een driehoek is, moeten we het eens zijn over wat we bedoelen met punten en lijnen. We werken aan sferische meetkunde (letterlijk meetkunde op het oppervlak van een bol)., In deze meetkunde is de ruimte het oppervlak van de bol; de punten zijn punten op dat oppervlak, en de lijn van Kortste Afstand tussen twee punten is de grootcirkel die de twee punten bevat. Een grootcirkel (zoals de evenaar) snijdt de bol in twee gelijke hemisferen. Deze geometrie heeft duidelijke toepassingen op afstanden tussen plaatsen en luchtroutes op aarde.,

draaiende bol met grootcirkel

de hoek tussen twee grote cirkels op een punt P is de Euclidische hoek tussen de richtingen van de cirkels (of strikt tussen de raaklijnen aan de cirkels op P). Dit levert geen problemen op in de navigatie op de Aarde, omdat we op een bepaald punt denken aan de hoek tussen twee richtingen alsof de Aarde vlak was op dat punt.

een lune is een deel van het oppervlak van de bol begrensd door twee grote cirkels die elkaar ontmoeten op antipodale punten., We kijken eerst naar de oppervlakte van een lune en dan introduceren we een andere grootcirkel die de lune in driehoeken splitst.

roterende bol met 4 lunes

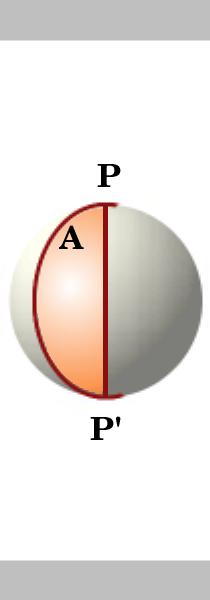
Lemma.

De oppervlakte van een lune op een cirkel met eenheidsradius is tweemaal zijn hoek, dat wil zeggen als de hoek van de lune A is dan is zijn oppervlakte 2A. twee grote cirkels die elkaar kruisen op antipodale punten P en P’ verdelen de bol in 4 lunes. De oppervlakte van het oppervlak van een eenheidsbol is $4\pi$.,

de gebieden van de lunes zijn evenredig met hun hoeken bij P, dus het gebied van een lune met hoek A is

${\frac{A}{2\pi}\times {4\pi}= {2A}}$

Oefening 1.

Wat zijn de gebieden van de andere 3 lunes? Komen jouw 4 gebieden overeen met $4 \ pi$?

Controleer hier uw antwoorden .

De zijden van een driehoek ABC zijn segmenten van drie grote cirkels die het oppervlak van de bol in acht bolvormige driehoeken snijden. Tussen de twee grote cirkels door het punt A zijn er vier hoeken., We labelen de hoek binnen driehoek ABC als hoek A, en ook de andere hoeken van driehoek ABC als hoek B en hoek C.

draaiende bol met 8 driehoeken

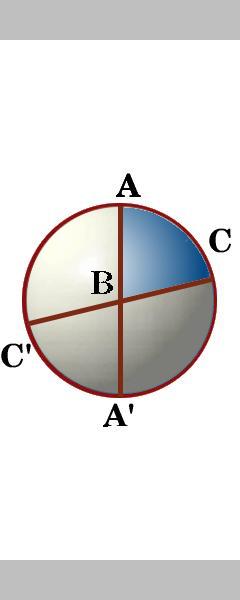
Oefening 2

roteren van de bol kunt u de acht driehoeken noemen en zeggen of een van hen hetzelfde gebied heeft? Bekijk hier uw antwoorden .

stelling.

beschouw een bolvormige driehoek ABC op de eenheidsbol met hoeken A, B en C. dan is de oppervlakte van driehoek ABC

A + B + C – $ \ pi$.,

het diagram toont een beeld dat neerkijkt op de hemisfeer met de lijn door AC als grens. De gebieden gemarkeerd Gebied 1 en gebied 3 zijn lunes met respectievelijk hoeken A en C. Denk aan de lunes door B en B’. Driehoek ABC is congruent aan driehoek A ‘B’ ‘dus het strikje vormige gearceerde gebied, gemarkeerd Gebied 2, dat is de som van de gebieden van de driehoeken ABC en een ‘BC’, is gelijk aan het gebied van de lune met hoek B, dat is gelijk aan 2B.,

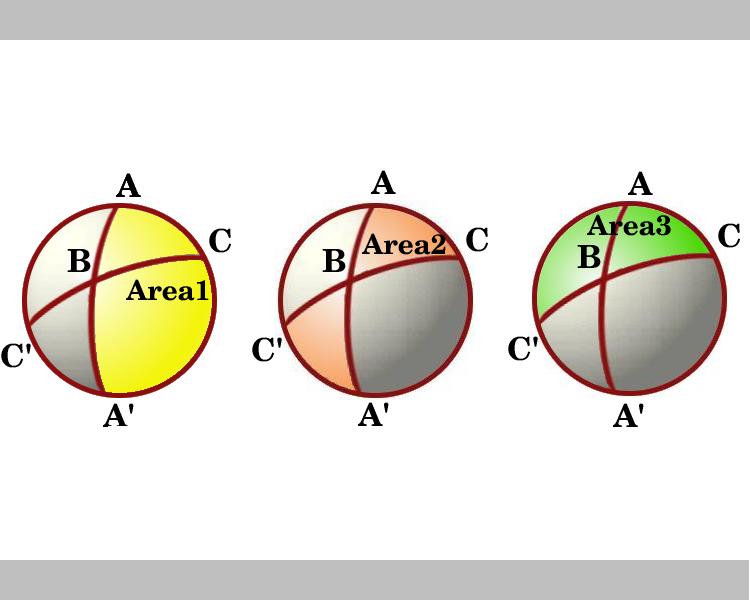
dus in het diagram zien we de gebieden van drie lunes en, met behulp van het lemma, deze zijn:

Gebied 1 = 2A
Gebied 2 = 2B
gebied 3 = 2C

bij het optellen van deze drie gebieden nemen we de oppervlakte van de driehoek ABC driemaal op., Hence

3., Niet-Euclidische meetkunde

soms zijn revolutionaire ontdekkingen niets meer dan het zien van wat er de hele tijd onder onze neus is geweest. Dit was het geval bij de ontdekking van de niet-Euclidische meetkunde in de negentiende eeuw. Ongeveer 2000 jaar nadat Euclides zijn ‘elementen’ schreef in 325 v.Chr. probeerden mensen het parallelle postulaat als een stelling in de meetkunde uit de andere axioma ‘ s te bewijzen, maar dat mislukte altijd en dat is een lang verhaal., Ondertussen gebruikten wiskundigen de hele tijd de sferische meetkunde, een meetkunde die de andere axioma ‘ s van de Euclidische meetkunde gehoorzaamt en veel van dezelfde stellingen bevat, maar waarin het parallelle postulaat niet geldt. Al die tijd hadden ze een voorbeeld van een niet-Euclidische meetkunde onder hun neus.

denk aan een lijn L en een punt P niet op L. De grote vraag is: “hoeveel lijnen kunnen door P worden getrokken evenwijdig aan L?`In de Euclidische meetkunde is het antwoord “precies één” en dit is één versie van het parallelle postulaat., Als de som van de hoeken van elke driehoek in de meetkunde $\pi$ radialen is dan geldt het parallelle postulaat en vice versa, de twee eigenschappen zijn equivalent.

in de sferische meetkunde zijn de basisaxioma ‘ s die we aannemen (de regels van het spel) verschillend van de Euclidische meetkunde – dit is een niet-Euclidische meetkunde. We hebben gezien dat in de sferische meetkunde de hoeken van driehoeken niet altijd optellen tot $\pi$ radialen dus we zouden niet verwachten dat het parallelle postulaat stand houdt., In de sferische meetkunde zijn de rechte lijnen (lijnen met de kortste afstand of geodesics)grote cirkels en snijdt elke lijn in de meetkunde elke andere lijn in twee punten. Het antwoord op de grote vraag over parallellen is ” als we een lijn L en een punt P niet op L dan zijn er geen lijnen door P evenwijdig aan de lijn L.,”

De Griekse wiskundigen (bijvoorbeeld Ptolemaeus C 150) berekenden de metingen van rechthoekige sferische driehoeken en werkten met formules van sferische trigonometrie en Arabische wiskundigen (bijvoorbeeld Jabir ibn Aflah c 1125 en Nasir ed-din C 1250) breidden het werk nog verder uit. De formule die in dit artikel wordt besproken werd ontdekt door Harriot in 1603 en gepubliceerd door Girard in 1629. Verdere ideeën over het onderwerp werden ontwikkeld door Saccerhi (1667 – 1733).,

dit alles werd grotendeels onopgemerkt door de 19e-eeuwse ontdekkers van de hyperbolische meetkunde, een andere niet-Euclidische meetkunde waar het parallelle postulaat niet geldt. In de sferische meetkunde (ook wel elliptische meetkunde genoemd) tellen de hoeken van driehoeken samen tot meer dan $\pi$ radialen en in de hyperbolische meetkunde tellen de hoeken van driehoeken samen tot minder dan $\pi$ radialen.

voor meer informatie zie het artikel van Alan Beardon ‘ hoeveel geometrieën zijn er?’en het artikel van Keith Carne ‘Strange Geometries’., Er zijn enkele praktische activiteiten die u zelf kunt proberen om deze geometrieën verder te verkennen te vinden op http://nrich.maths.org/MOTIVATE/conf8/index.html