kans op het rollen van twee dobbelstenen

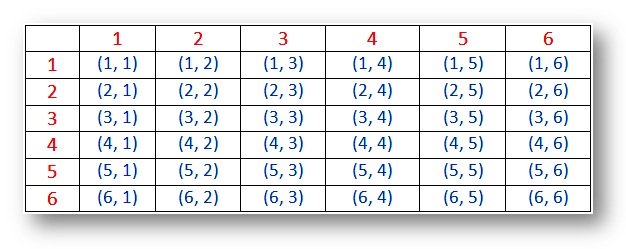
opmerking:

(i) de uitkomsten (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) en (6, 6) worden doublets genoemd.

(ii) het paar (1, 2) en (2, 1) zijn verschillende uitkomsten.

uitgewerkte problemen met betrekking tot de waarschijnlijkheid van het werpen van twee dobbelstenen:

1. Twee dobbelstenen worden gegooid. Laat a, B, C de gebeurtenissen zijn van het krijgen van een som van 2, een som van 3 en een som van 4 respectievelijk., Laat vervolgens zien dat

(i) A een eenvoudige gebeurtenis is

(ii) B en C zijn samengestelde gebeurtenissen

(iii) A en B sluiten elkaar uit

oplossing:

duidelijk hebben we
A = {(1, 1)}, B = {(1, 2), (2, 1)} en C = {(1, 3), (3, 1), (2, 2)}.

(i) aangezien A uit één monsterpunt bestaat, is het een eenvoudige gebeurtenis.

(ii) aangezien zowel B als C meer dan één monsterpunt bevatten, is elk van hen een samengestelde gebeurtenis.

(iii) aangezien A B B = ∅, sluiten A en B elkaar uit.

2. Twee dobbelstenen worden gegooid., A is de gebeurtenis dat de som van de getallen weergegeven op de twee dobbelstenen is 5, en B is de gebeurtenis dat ten minste een van de dobbelstenen toont een 3. zijn de twee gebeurtenissen (i) elkaar uitsluiten, (ii) uitputtend? Geef argumenten ter ondersteuning van uw antwoord.

oplossing:

wanneer twee dobbelstenen worden gegooid, hebben we n (S) = (6 × 6) = 36.

Nu, A = {(1, 4), (2, 3), (4, 1), (3, 2)}, en

B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}

(i) a ∩ B = {(2, 3), (3, 2)} ≠ ∅.

daarom sluiten A en B elkaar niet uit.,

(ii) ook A ∪ B ≠ S.

daarom zijn A en B geen exhaustieve gebeurtenissen.

meer voorbeelden gerelateerd aan de vragen over de kansen om twee dobbelstenen te gooien.

3. Twee dobbelstenen worden tegelijkertijd gegooid.,) het krijgen van een doublet

(v) het krijgen van een som van 8

(vi) aan de som deelbaar is door 5

(vii) aan de som van tenminste 11

(viii) aan een veelvoud van 3 als de som

(ix) het krijgen van een totaal van minstens 10

(x) een oneven getal als de som

(xi) het krijgen van een priemgetal als de som

(xii) het krijgen van een doublet van even getallen

(xiii) het krijgen van een veelvoud van 2 op een dobbelsteen en een veelvoud van 3 op de andere dobbelsteen

Oplossing:

Twee verschillende dobbelstenen worden gegooid tegelijkertijd wordt de nummer 1, 2, 3, 4, 5 en 6 op hun gezichten., We weten dat in een enkele gegooid van twee verschillende dobbelstenen, het totale aantal mogelijke uitkomsten is (6 × 6) = 36.

(i) zes krijgen als product:

laat E1 = het geval van zes krijgen als product. Het getal waarvan het product zes is, is E1 = = 4

daarom is de kans dat ‘six as a product’

aantal gunstige uitkomsten
P(E1) = totaal aantal mogelijke uitkomsten
= 4/36
= 1/9

(ii) Som ≤ 3 krijgen:

laat E2 = event van Som ≤ 3 krijgen., Het aantal waarvan de som ≤ 3 is E2 = = 3

daarom is de kans dat ‘Som ≤ 3’

aantal gunstige uitkomsten
P(E2) = totaal aantal mogelijke uitkomsten
= 3/36
= 1/12

(iii) Som ≤ 10 krijgen:

laat E3 = gebeurtenis van Som ≤ 10 krijgen. Het getal waarvan de som ≤ 10 is E3 =

= 33

daarom is de kans dat ‘Som ≤ 10’

aantal gunstige uitkomsten
P(E3) = totaal aantal mogelijke uitkomsten
= 33/36
= 11/12
(iv)een doublet krijgt:laat E4 = het geval van een doublet krijgen., Het aantal dat doublet zal zijn E4 = = 6

daarom is de kans dat’een doublet’

aantal gunstige uitkomsten
P (E4)= totaal aantal mogelijke uitkomsten
= 6/36
= 1/6

(v) een som van 8 krijgt:

laat E5 = event van het krijgen van een som van 8. Het getal dat een som van 8 is zal E5 = = 5

daarom is de kans dat ‘een som van 8’

aantal gunstige uitkomsten
P(E5) = totaal aantal mogelijke uitkomsten
= 5/36

(vi)som deelbaar door 5 krijgen:

laat E6 = gebeurtenis van Som deelbaar door 5 krijgen., Het getal waarvan de som deelbaar is door 5 is E6 = = 7

daarom is de kans dat’Som deelbaar door 5′

aantal gunstige uitkomsten
P(E6) = totaal aantal mogelijke uitkomsten
= 7/36

(vii)som van tenminste 11 krijgen:

laat E7 = gebeurtenis van som van tenminste 11 krijgen. De gebeurtenissen van de som van tenminste 11 zijn E7 = = 3

daarom is de kans dat ‘som van tenminste 11’

aantal gunstige uitkomsten
P(E7) = totaal aantal mogelijke uitkomsten
= 3/36
= 1/12

(viii) een veelvoud van 3 krijgt als de som:

zij E8 = gebeurtenis van het krijgen van een veelvoud van 3 als de som., De gebeurtenissen van een veelvoud van 3 als de som zijn E8 = = 12

daarom is de kans dat ‘een veelvoud van 3 als de som’

aantal gunstige uitkomsten
P(E8) = totaal aantal mogelijke uitkomsten
= 12/36
= 1/3

(ix) een totaal van ten minste 10 krijgt:

laat E9 = gebeurtenis van een totaal van ten minste 10 krijgen., De gebeurtenissen van een totaal van tenminste 10 zullen E9 = = 6

daarom is de kans dat ‘een totaal van tenminste 10’

aantal gunstige uitkomsten
P (E9)= totaal aantal mogelijke uitkomsten
= 6/36
= 1/6

(x) een evennummer krijgt als de som:

laat E10 = gebeurtenis van het krijgen van een even getal als de som., De gebeurtenissen van een even getal als de som zijn E10 = = 18

daarom is de kans dat ‘een even getal als de som

aantal gunstige uitkomsten
P (E10)= totaal aantal mogelijke uitkomsten
= 18/36
= 1/2

(xi) een primenumber als de som krijgen:

laat E11 = gebeurtenis van het krijgen van een priemgetal als de som., De gebeurtenissen van een priemgetal als de som zijn E11 = = 15

daarom is de kans op het krijgen van’een priemgetal als de som’

aantal gunstige uitkomsten
P(E11) = totaal aantal mogelijke uitkomsten
= 15/36
= 5/12

(xii) het krijgen van een dubbele even getallen:

laat E12 = gebeurtenis van het krijgen van een dubbele even getallen., De gebeurtenissen van een doublet van even getallen worden E12 = = 3

Dus, de kans ofgetting ‘een doublet van even getallen’

Aantal gunstige uitkomsten
P(E12) = Totaal aantal mogelijke uitkomst
= 3/36
= 1/12

(xiii) aan de amultiple van 2 op een dobbelsteen en een veelvoud van 3 op de andere sterven:

Laten we E13 = gebeurtenis van het krijgen van een veelvoud van 2 op een dobbelsteen en een veelvoud van 3 op de andere dobbelsteen., De gebeurtenissen van een veelvoud van 2 op de ene matrijs en een veelvoud van 3 op de andere matrijs zijn E13 = = 11

daarom is de kans dat ‘een veelvoud van 2 op de ene matrijs en een veelvoud van 3 op de andere matrijs’

aantal gunstige uitkomsten
P(E13) = totaal aantal mogelijke uitkomsten
= 11/36

4. Tweedice worden gegooid. Zoek (i) de kansen in het voordeel van het krijgen van de som 5, en (ii) theodds tegen het krijgen van de som 6.

oplossing:

we weten dat in een enkele worp van twee dobbelstenen het totale aantal mogelijke uitkomsten (6 × 6) = 36 is.

zij de monsterruimte. Dan, n ( S) = 36.,

(i) de kansen in het voordeel van het krijgen van de som 5:

zij E1 de gebeurtenis van het krijgen van de som 5. Dan,
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒ P (E1) = 4
daarom P (E1) = n (E1)/n ( S) = 4/36 = 1/9
⇒ odds in het voordeel van E1 = P(E1)/ = (1/9)/(1 – 1/9) = 1/8.

(ii) de kans op het krijgen van de som 6:

laat E2 de gebeurtenis zijn van het krijgen van de som 6. Dan,
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒ P (E2) = 5
daarom P(E2) = n (E2)/n (S) = 5/36
⇒ odds tegen E2 = /P (E2) = (1 – 5/36)/(5/36) = 31/5.

5., Twee dobbelstenen, een blauwe en een oranje, worden tegelijkertijd gegooid. Zoek de kans op het krijgen van

(i) gelijke getallen op beide

(ii) twee getallen die op hen verschijnen waarvan de som 9 is.,

Oplossing:

De mogelijke uitkomsten zijn

(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)

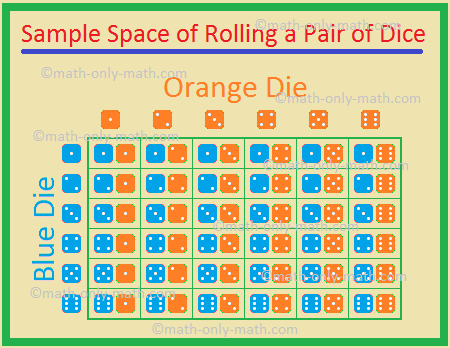
hierdoor is het totale aantal mogelijke uitkomsten = 36.,

(i) aantal gunstige resultaten voor de gebeurtenis E

= aantal resultaten met gelijke getallen op beide dobbelstenen

= 6 .

dus, per definitie, P (E) = \(\frac{6}{36}\)

= \(\frac{1}{6}\)

(ii) aantal gunstige resultaten voor de gebeurtenis F

= Aantal resultaten waarbij twee getallen die erop voorkomen de som hebben 9

= 4 .

dus, per definitie, P (F) = \(\frac{4}{36}\)

= \(\frac{1}{9}\).

deze voorbeelden zullen ons helpen om verschillende soorten problemen op te lossen op basis van de waarschijnlijkheid voor het rollen van twee dobbelstenen.,p>Probability and Playing Cards

Probability for Rolling Two Dice

Solved Probability Problems

Probability for Rolling Three Dice

9th Grade Math

From Probability for Rolling Two Dice to HOME PAGE