vectoren zijn uitgebreid nuttig in de wetenschap om alles te beschrijven dat zowel een richting als een magnitude heeft. Ze worden meestal getekend met behulp van puntige pijlen, waarvan de lengte de magnitude van de vector vertegenwoordigt. Een quarterback pass is het eenvoudige voorbeeld omdat het de richting meestal ergens downfield en een magnitude. Soms moeten we met twee vectoren samen aan een object werken. In dergelijke gevallen zijn hoeken tussen die vectoren belangrijk., Dit onderwerp zal de hoek tussen twee vectoren formule evenals voorbeelden uitleggen. Laten we het leren!
Concept vectoren
buiten het veld kunnen vectoren worden gebruikt om een willekeurig aantal fysieke objecten of activiteiten weer te geven. Bijvoorbeeld. Wind, bijvoorbeeld, is een vectoriële hoeveelheid. Het is omdat op een bepaalde locatie het heeft een richting en de grootte. We kunnen een kaart maken van de luchtstroom op elk moment, dan, door de windvectoren te tekenen voor een aantal verschillende geografische locaties.
veel eigenschappen van bewegende objecten zijn ook een soort vectoren., In biljartbal beschrijft zijn snelheidsvector zijn beweging. Het toont de richting van de vector pijl markeert als de richting van de beweging, en de lengte van de vector vertegenwoordigt de snelheid van de bal.
het momentum van de biljartbal is ook een voorbeeld van vectoriële grootheid. Zoals het gelijk is aan massa maal snelheid. Daarom is de momentumvector van de kogelpunten in dezelfde richting als zijn snelheidsvector. En de magnitude van de momentumvector zal het vermenigvuldigingsproduct zijn van de snelheid en de massa van de bal.,
in termen van wiskunde is een vector elk object dat een definieerbare magnitude en richting heeft. Omdat vectoren niet hetzelfde zijn als standaardlijnen of vormen, moeten we een aantal speciale formules gebruiken om hoeken tussen hen te vinden.
de formule voor de hoek tussen twee vectoren
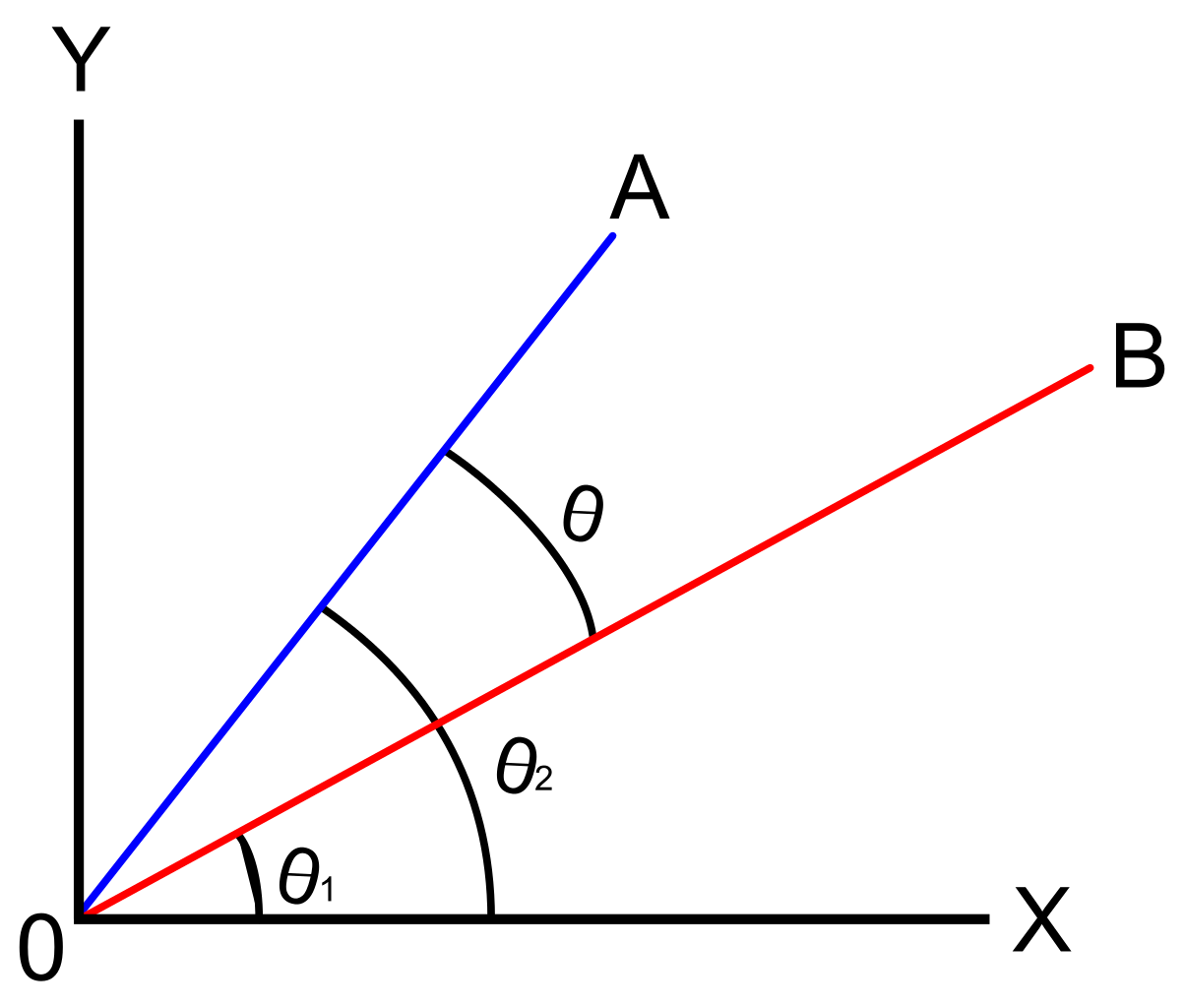
de hoek tussen twee vectoren zal worden uitgesteld door een enkel punt, dat wordt genoemd als de kortste hoek waarbij we een van de vectoren moeten draaien naar de positie van co-directionele met een andere vector.,
de discussie over richtingshoeken van vectoren richt zich op het vinden van de hoek van een vector ten opzichte van de positieve x-as. Dit zal zich richten op de hoek tussen twee vectoren in de standaardpositie. Van een vector wordt gezegd dat hij zich in de standaardinstelling bevindt als zijn beginpunt de oorsprong is (0, 0).
als de twee vectoren worden aangenomen als a en b dan wordt de gecreëerde punt gedefinieerd als a .b.laten we aannemen dat deze twee vectoren gescheiden zijn door hoek \(\theta\). Om te weten wat de hoekmeting is zullen we oplossen met behulp van de formule gegeven:
We kennen het dot product:
\(\vec{a}.,\vec{b} ||\vec{a}||\vec{b}/cos\theta\)
nu is de hoek tussen twee vectoren formule:
\(\theta = cos^{-1}\frac{\vec{a}.\vec{b}} {|\vec{a}||\vec{b}/}\)
waarbij \\(theta\) de hoek tussen A-en b-vectoren is.
opgeloste voorbeelden voor hoek tussen twee vectoren formule
Q. 1: Bereken de hoek tussen twee vectoren 3i + 4j-k en 2i-j + k.
oplossing: Let,
a = 3i + 4j-k en
b = 2i – j + k
We definiëren het dotproduct als:
a .b = (3i + 4j-k).(2i – j + k)
















Geef een reactie