Driehoek Figuur Hoek-Zijde-Hoek (ASA)
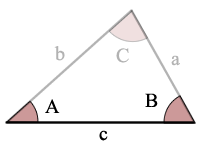
A = hoek A
B = hoek B
C = hoek C
a = kant een
b = b-kant
c = zijde c
P = omtrek
s = semi-omtrek
K) = oppervlakte
r = straal van de ingeschreven cirkel
R = straal van de omgeschreven cirkel
Rekenmachine Gebruiken
Elke berekening optie, hieronder weergegeven, heeft sub-kogels die lijst de volgorde van de methoden die gebruikt zijn in deze calculator op te lossen voor het onbekende hoek en kant-waarden waaronder de Som van de Hoeken in een Driehoek, de Wet van de Sinussen en de Wet van Gezelligheid., Dit zijn niet de enige sequenties die je kunt gebruiken om dit soort problemen op te lossen.
- zie ook deze Trigonometriecalculators:
- wet van de Cosinuscalculator
- wet van de Sinuscalculator
oplossende Driehoeksstellingen
AAA is Hoek, Hoek, Hoek
het specificeren van de drie hoeken van een driehoek geeft niet op unieke wijze één driehoek aan. Daarom, het specificeren van twee hoeken van een tringle kunt u de derde hoek alleen berekenen.,
gegeven de grootte van 2 hoeken van een driehoek kunt u de grootte van de derde hoek berekenen. Het totaal is gelijk aan 180 ° of π radialen.
C = 180° – A-B (in graden)
C = π-A-B (in radialen)
AAS is Hoek, Hoek, zijde
gegeven de grootte van 2 hoeken en 1 zijde tegenover een van de gegeven hoeken, kunt u de grootte van de resterende 1 hoek en 2 zijden berekenen.
gebruik de som van hoeken regel om de andere hoek te vinden, dan
gebruik de wet van Sines om op te lossen voor elk van de andere twee zijden.,
ASA is Hoek, zijde, hoek
gegeven de grootte van 2 hoeken en de grootte van de zijde die zich tussen deze 2 hoeken bevindt, kunt u de grootte van de resterende 1 hoek en 2 zijden berekenen.
gebruik de som van hoeken regel om de andere hoek te vinden, dan
gebruik de wet van Sines om op te lossen voor elk van de andere twee zijden.,
ASS (of SSA) is Hoek, zijde, zijde
gegeven de grootte van 2 zijden (a en c Waar a < c) en de grootte van de hoek A die niet tussen deze 2 zijden ligt, kunt u misschien de grootte van de resterende 1 zijde en 2 hoeken berekenen, afhankelijk van de volgende voorwaarden.,f Gezelligheid op te lossen voor elk van de andere twee hoeken
aanwezig 2 volledige oplossingen
Voorbeeld: 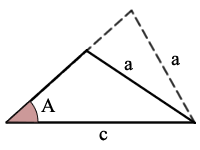
sin(A) = a/c, er is één van de mogelijke driehoek
gebruik De Wet van Sines te lossen voor een hoek, C
gebruik de Som van de Hoeken Regel te vinden in de andere hoek, B
gebruik De Wet van Sines te lossen voor de laatste zijde, b
Voorbeeld: 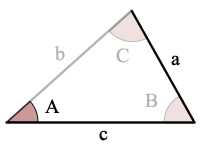
sin(A) > a/c, er zijn geen mogelijke driehoeken
Fout Aankondiging: sin(A) > a/c zodat er geen oplossingen zijn en geen driehoek!,
voorbeeld: 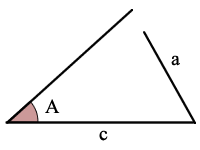
SAS is zijde, hoek, zijde
gegeven de grootte van 2 zijden (c en a) en de grootte van de hoek B die tussen deze 2 zijden ligt, kunt u de grootte van de resterende 1 zijde en 2 hoeken berekenen.
gebruik de Cosinuswet om op te lossen voor de resterende zijde, b
bepaal welke zijde, a of c, het kleinst is en gebruik de Sinuswet om op te lossen voor de grootte van de tegenoverliggende hoek, respectievelijk A of C.,
gebruik de Sum of Angles regel om de laatste hoek
te vinden SSS is Side, Side, Side
gegeven de grootte van de 3 zijden kunt u de grootte van alle 3 hoeken in de driehoek berekenen.
gebruik de Cosinuswet om de hoeken op te lossen. Je zou ook de som van hoeken regel kunnen gebruiken om de uiteindelijke hoek te vinden als je eenmaal Weet 2 van hen.,sin-1
de Wet van Cosinussen
Als a, b en c zijn de lengten van de benen van een driehoek tegenover de hoeken A, B en C respectievelijk; dan is het recht van gezelligheid staten:
a2 = c2 + b2 – 2bc cos A, voor het oplossen van cos A cos A = ( b2 + c2 – a2 ) / 2bc
b2 = a2 + c2 – 2ca cos B, voor het oplossen van cos B cos B = ( c2 + a2 – b2 ) / 2ca
c2 = b2 + a2 – 2ab cos C, voor het oplossen van cos C, cos C = ( a2 + b2 – c2 ) / 2ab
op te Lossen, bijvoorbeeld voor een hoek, A = cos-1
Andere Driehoek Kenmerken
Driehoek omtrek, P = a + b + c
Driehoek semi-omtrek, s = 0.,5 * (a + b + c)
driehoek gebied, K = √
straal van ingeschreven cirkel in de driehoek, r = √
straal van omschreven cirkel rond driehoek, R = (abc) / (4K)
referenties/ verdere lezing
Weisstein, Eric W. “Ass stelling.”Van MathWorld — Een Wolfram Web Resource. KONTSTELLING.
Math is Fun-Solving Sas driehoeken
















Geef een reactie