convexe en Concave veelhoeken

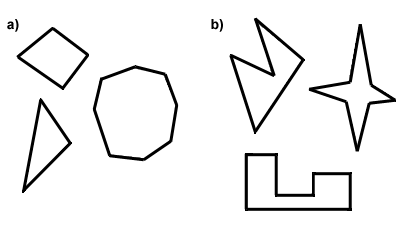
elke veelhoek is ofwel convex of concaaf. Het verschil tussen convexe en concave polygonen ligt in de maten van hun hoeken. Om een veelhoek convex te laten zijn, moeten alle inwendige hoeken minder dan 180 graden zijn. Anders is de veelhoek concave. Een andere manier om er over te denken is dit: de diagonalen van een convexpolygoon zullen allemaal in het binnenste van de veelhoek zijn, terwijl bepaalde diagonalen van een concave veelhoek buiten de veelhoek zullen liggen, aan de buitenkant., Below in Part A are some convex polygons, and in Part B, some concave polygons. In the rest of this text, you can assume that every polygon discussed is convex.

Figure %: Convex and concave polygons

Regular Polygons

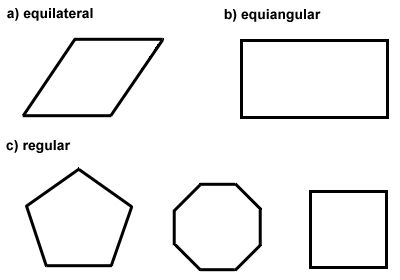
Polygons can also be classified as equilateral, equiangular, or both. Equilateral polygons have congruent sides, like a rhombus. Equiangular polygons have congruent interior angles, like a rectangle., Wanneer een veelhoek zowel gelijkzijdig als equiangulair is, wordt het een regelmatige veelhoek genoemd. Een vierkant is een voorbeeld van een regelmatige veelhoek. Het centrum van een regelmatige veelhoek is het punt van waaruit alle hoekpunten van de veelhoek op gelijke afstand liggen. Regelmatige polygonen hebben speciale eigenschappen die we in de volgende sectie zullen onderzoeken. Hieronder zijn enkele voorbeelden van equiangular, equilateral, en regelmatige veelhoeken.,

Figure %: Equilateral, equiangular, and regular polygons

Congruent Polygons

One more note on polygons: Polygons whose sides are all congruent are congruent polygons. Knowing this term will be important later. In congruent polygons, every segment is congruent.