een vector heeft magnitude (hoe lang het is) en richting:
Hier zijn twee vectoren:

ze kunnen worden vermenigvuldigd met het “Dot Product” (zie ook Cross Product).,
Wij kunnen het berekenen van het Scalair Product van twee vectoren op deze manier:

a · b = |a| × |b| × cos(θ)
Waar:
|a| is de omvang (lengte) van de vector a
|b| is de grootte (lengte) van de vector b
θ is de hoek tussen a en b.
Dus we vermenigvuldigen de lengte maal de lengte van b, dan vermenigvuldigen met de cosinus van de hoek tussen a en b.
OF kunnen we berekenen het op deze manier:
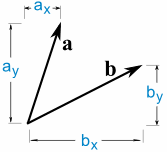
a · b = ax × bx + ay × door
Dus we vermenigvuldigen de x -, vermenigvuldig de y ‘ s en vervolgens op toevoegen.,
beide methoden werken!
en het resultaat is een getal (een “scalar” genoemd, dus we weten dat het geen vector is).
Opmerking: U kunt de Vectorcalculator gebruiken om u te helpen.
waarom cos(θ) ?
OK, om twee vectoren te vermenigvuldigen is het zinvol om hun lengtes samen te vermenigvuldigen, maar alleen als ze in dezelfde richting wijzen.,
Dus maken we een “punt in dezelfde richting”, zoals de andere door te vermenigvuldigen met cos(θ):
 |
 |
|
| We nemen het onderdeel van een dat ligt naast de b |
Als er scheen een licht om te zien waar de schaduw ligt |
VERVOLGENS vermenigvuldigen we !,
rechte hoeken
wanneer twee vectoren loodrecht op elkaar staan, is het puntproduct nul.
dit kan een handige manier zijn om erachter te komen of twee vectoren loodrecht staan.
drie of meer dimensies
dit alles werkt ook prima in 3 (of meer) dimensies.
en kan eigenlijk heel nuttig zijn!
Ik heb een keer zo ‘ n berekening geprobeerd, maar werkte allemaal in hoeken en afstanden … het was erg moeilijk, met veel trigonometrie, en mijn hersenen deden pijn. De bovenstaande methode is veel gemakkelijker.,
Cross Product
Het Dotproduct geeft een scalair (gewoon getal) antwoord, en wordt soms het scalaire product genoemd.
maar er is ook het kruisproduct dat een vector als antwoord geeft, en soms het vectorproduct wordt genoemd.

















Geef een reactie