Men. Ik heb het gevoel dat ik het leuk vind wat je zegt.
Soc. En ik, Meno, hou van wat ik zeg.
van Plato ‘ s Meno
De lengte van de diagonaal van het eenheidsvierkant is gelijk aan de vierkantswortel van 2.
De lengte van de diagonaal van het eenheidsvierkant is gelijk aan √2. Dit is niet echt geweldig nieuws. Iedereen die ooit de stelling van Pythagoras tegenkwam, is zich daarvan bewust., In de gelijkbenige rechthoekige driehoek met de poten van lengte 1, is de hypotenusa, volgens de stelling van Pythagoras – 12 + 12 = (hypotenusa)2 – inderdaad van lengte √2. De motivatie voor deze pagina is niet zozeer dat feit zelf, maar de manier om het te laten zien zonder een beroep op de beroemde stelling. Inderdaad, men zou kunnen stellen dat de stelling van Pythagoras misschien overmatig is gebruikt, zie een merkwaardig voorbeeld.een argument dat teruggaat op de figuur die Socrates in Plato ‘ s Meno heeft getekend, zou Pythagoras zelf bekend kunnen zijn geweest, hoewel de laatste een eeuw eerder leefde.,
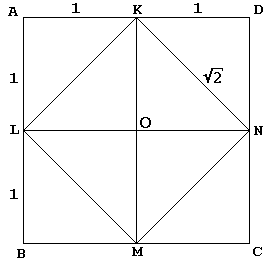
in het dialoogvenster leidt Socrates, op zijn gebruikelijke manier, een jonge slaaf naar een constructie van een vierkant twee keer de oppervlakte van de gegeven:
het gegeven vierkant KLMN met Centrum O wordt eerst door zijn diagonalen in 4 gelijke driehoeken gesneden. Socrates integreert KLMN in een groter vierkant ABCD alsof het deze driehoeken reflecteert elk in zijn schuine zijde. De slaaf geeft dan toe-en wie niet? – dat vierkant ABCD is twee keer zo groot als vierkant KLMN.
eerlijk gezegd, Socrates’ vierkant ABCD gemeten 4 aan de zijkant, zodat vierkant KLMN had oppervlakte van 8., Het is duidelijk dat wanneer we beginnen met het vierkant ABCD van kant 2 (en dus van gebied 4), vierkant KLMN een oppervlakte van 2 zal hebben.
nu, in het algemeen, voor een positief getal A, √A wordt gedefinieerd als een getal waarvan het kwadraat A is:
(√A)2.
aan de andere kant, elke student van gebieden weet, dat de oppervlakte van een vierkant van kant b gelijk is aan b2. Hieruit volgt dat de zijde van een vierkant met oppervlakte A precies √A. we concluderen dat de zijde van het vierkant KLMN gelijk is aan √2. Voor een,
KN = √A.
het centrale punt van het argument is het feit dat, in het diagram, KN een dubbele rol speelt., Naast het feit dat een van de zijden van vierkant KLMN, het dient ook als een diagonaal van vierkant OKDN. Dit laatste is natuurlijk een eenheidsvierkant, wat onze bewering bewijst.
(vanuit een ander perspectief wordt dezelfde episode elders genoemd.)
















Geef een reactie