mobiele notitie tonen Toon alle notities Verberg alle notities
sectie 3-1: parametrische vergelijkingen en krommen
tot op dit punt (in zowel Calculus I als Calculus II) hebben we bijna uitsluitend gekeken naar functies in de vorm \(y = f\left( x \right)\) of \(x = H\left( y \right)\) en bijna alle formules die we hebben ontwikkeld vereisen dat functies in een van deze twee vormen zijn. Het probleem is dat niet alle curves of vergelijkingen die we willen bekijken gemakkelijk in deze vorm vallen.
Neem bijvoorbeeld een cirkel. Het is gemakkelijk genoeg om de vergelijking van een cirkel gecentreerd op de oorsprong met straal \(r\) op te schrijven.,
\
echter, we zullen nooit in staat zijn om de vergelijking van een cirkel neer te schrijven als een enkele vergelijking in een van de bovenstaande vormen. Zeker kunnen we oplossen voor \(x\) of \(y\) omdat de volgende twee formules
\
laten zien, maar er zijn in feite twee functies in elk van deze. Elke formule geeft een deel van de cirkel.
\
helaas werken we meestal aan de hele cirkel, of kunnen we gewoon niet zeggen dat we slechts aan één deel ervan werken. Zelfs als we kunnen beperken tot slechts een van deze delen van de functie is nog steeds vaak vrij onaangenaam om mee te werken.,
\
deze derde variabele wordt meestal aangeduid met \(t\) (zoals we hier deden) maar hoeft dat natuurlijk niet te zijn. Soms beperken we de waarden van \(t\) die we zullen gebruiken en op andere momenten niet. dit zal vaak afhankelijk zijn van het probleem en wat we proberen te doen.
om te helpen visualiseren wat een parametrische curve is, doe alsof we een grote watertank hebben die constant in beweging is en we laten een pingpongbal in de tank vallen., Het punt \(\left ({x,y} \right) = \left ({f\left( t \right),g\left(T \right)} \right)\) geeft dan de locatie weer van de pingpongbal in de tank op tijd \(t\) en de parametrische curve is een spoor van alle locaties van de pingpongbal. Merk op dat dit niet altijd een correcte analogie is, maar het is in eerste instantie nuttig om te helpen visualiseren wat een parametrische curve is.
het schetsen van een parametrische curve is niet altijd gemakkelijk. Laten we eens kijken naar een voorbeeld om een manier te zien om een parametrische curve te schetsen., Dit voorbeeld zal ook illustreren waarom deze methode is meestal niet de beste.
Op dit punt is onze enige optie voor het schetsen van een parametrische curve om waarden van \(t\) te kiezen, ze in de parametrische vergelijkingen te steken en dan de punten te plotten. Dus, laten we plug in sommige \(t\) ‘ s.,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Helaas is er op dit moment geen echt antwoord op deze vraag. We kiezen gewoon \(t\)’s totdat we er vrij zeker van zijn dat we een goed idee hebben van hoe de curve eruit ziet. Het is dit probleem met het kiezen van” goede ” waarden van \(t\) dat deze methode van het schetsen van parametrische krommen een van de armere keuzes maakt. Soms hebben we geen keus, maar als we wel een keuze hebben, moeten we die vermijden.
We zullen een alternatieve grafische methode bespreken in latere voorbeelden die zullen helpen om uit te leggen hoe deze waarden van \(t\) werden gekozen.,
we hebben nog een idee om te bespreken voordat we de curve daadwerkelijk schetsen. Parametrische krommen hebben een bewegingsrichting. De bewegingsrichting wordt gegeven door \(t\) te verhogen. Dus, bij het plotten van parametrische krommen, nemen we ook pijlen op die de bewegingsrichting aangeven. We geven vaak ook de waarde van \(t\) die specifieke punten op de grafiek gaf om de waarde van \(t\) die dat specifieke punt gaf duidelijk te maken.
Hier is de schets van deze parametrische kromme.
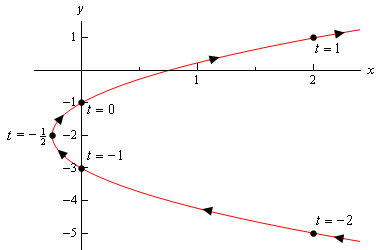
dus, het lijkt erop dat we een parabool hebben die naar rechts opent.,
voordat we dit voorbeeld beëindigen is er een enigszins belangrijk en subtiel punt dat we eerst moeten bespreken. Merk op dat we een gedeelte van de schets rechts van de punten hebben opgenomen die overeenkomen met \(t = – 2\) en \(t = 1\) om aan te geven dat er delen van de schets zijn. Als we gewoon de schets op die punten hadden gestopt geven we aan dat er geen deel van de curve aan de rechterkant van die punten was en dat zal er duidelijk zijn. We hebben alleen geen van die punten berekend.,
Dit lijkt misschien een onbelangrijk punt, maar zoals we in het volgende voorbeeld zullen zien is het belangrijker dan we zouden denken.
voordat we een veel eenvoudiger manier aanpakken om deze grafiek te schetsen, laten we eerst het probleem van limieten op de parameter aanpakken. In het vorige voorbeeld hadden we geen limieten op de parameter. Zonder beperkingen op de parameter zal de grafiek verder gaan in beide richtingen zoals weergegeven in de schets hierboven.
We zullen vaak limieten hebben op de parameter en dit zal de schets van de parametrische vergelijkingen beïnvloeden., Om dit effect te zien laten we kijken een lichte variatie van het vorige voorbeeld.
merk op dat het enige verschil hier de aanwezigheid van de limieten op \(t\) is. Al deze limieten vertellen ons dat we geen waarde van \(t\) buiten dit bereik kunnen nemen. Daarom zal de parametrische kromme slechts een deel van de bovenstaande kromme zijn. Hier is de parametrische kromme voor dit voorbeeld.,
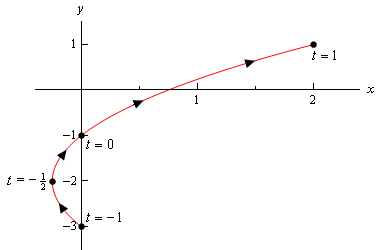
merk op dat we met deze schets de schets begonnen en gestopt hebben op de punten die afkomstig zijn van de eindpunten van het bereik van \(t\)’s. Vergelijk dit met de schets in het vorige voorbeeld waar we een deel van de schets hadden rechts van de” begin “en” eind ” punten die we berekenden.
in dit geval begint de kromme bij \(t = – 1\) en eindigt op \(t = 1\), terwijl in het vorige voorbeeld De Kromme niet echt begon op de juiste punten die we berekenden., We moeten duidelijk zijn in onze schetsen of de curve begint/eindigt op een punt, of dat dat punt was gewoon de eerste/laatste die we berekend.
Het is nu tijd om te kijken naar een eenvoudiger methode om deze parametrische curve te schetsen. Deze methode maakt gebruik van het feit dat we in veel, maar niet alle gevallen de parameter uit de parametrische vergelijkingen kunnen verwijderen en een functie krijgen die alleen \(x\) en \(y\) omvat. We zullen dit soms de algebraïsche vergelijking noemen om het te onderscheiden van de oorspronkelijke parametrische vergelijkingen., Er zullen twee kleine problemen zijn met deze methode, maar het zal gemakkelijk zijn om die problemen aan te pakken. Het is echter belangrijk op te merken dat we dit niet altijd kunnen doen.
hoe we de parameter elimineren zal afhangen van de parametrische vergelijkingen die we hebben. Laten we eens kijken hoe we de parameter voor de set van parametrische vergelijkingen die we hebben gewerkt met dit punt te elimineren.
een schets krijgen van de parametrische curve als we de parameter hebben geëlimineerd lijkt vrij eenvoudig. Het enige wat we moeten doen is een grafiek maken van de vergelijking die we vonden door de parameter te elimineren., Zoals reeds opgemerkt zijn er echter twee kleine problemen met deze methode. De eerste is de richting van de beweging. De vergelijking met alleen \(x\) en \(y\) geeft niet de bewegingsrichting van de parametrische kromme. Dit is over het algemeen een eenvoudig probleem op te lossen echter. Laten we eens snel kijken naar de afgeleiden van de parametrische vergelijkingen uit het laatste voorbeeld. Ze zijn,
\
merk op dat de \(x\) afgeleide niet zo nuttig is voor deze analyse als het zowel positief als negatief zal zijn en dus \(x\) zowel zal toenemen als afnemen afhankelijk van de waarde van \(t\)., Dat helpt niet veel met richting, omdat het volgen van de curve in beide richtingen zowel stijgend als dalend \(x\) zal vertonen.
in sommige gevallen zal slechts één van de vergelijkingen, zoals dit voorbeeld, de richting geven, terwijl in andere gevallen een van beide kan worden gebruikt. Het is ook mogelijk dat in sommige gevallen beide derivaten nodig zijn om de richting te bepalen. Het zal altijd afhankelijk zijn van de individuele verzameling parametrische vergelijkingen.,
het tweede probleem met het elimineren van de parameter kan het best worden geïllustreerd in een voorbeeld omdat we dit probleem zullen tegenkomen in de overige voorbeelden.
Oké, dat was een heel lang voorbeeld. De meeste van dit soort problemen zijn niet zo lang. We hadden gewoon veel te bespreken in deze, zodat we een paar belangrijke ideeën uit de weg konden krijgen. De rest van de voorbeelden in deze sectie zou niet zo lang moeten duren om door te gaan.
laten we nu eens kijken naar een ander voorbeeld dat een belangrijk idee over parametrische vergelijkingen zal illustreren.,
dus, we zagen in de laatste twee voorbeelden twee sets van parametrische vergelijkingen die op een bepaalde manier dezelfde grafiek gaven. Maar omdat ze de grafiek een ander aantal keren hebben getraceerd, moeten we ze echt zien als verschillende parametrische curves, tenminste op een bepaalde manier. Dit lijkt misschien een verschil waar we ons geen zorgen over hoeven te maken, maar zoals we later zullen zien, kan dit een heel belangrijk verschil zijn. In sommige van de latere secties hebben we een curve nodig die precies één keer wordt getraceerd.,
voordat we verder gaan met andere problemen laten we kort erkennen wat er gebeurt door het veranderen van de \(t\) naar een nt in dit soort parametrische vergelijkingen. Als we te maken hebben met parametrische vergelijkingen die alleen sines en cosines bevatten en die beiden hetzelfde argument hebben als we het argument van \(t\) naar nt veranderen, veranderen we gewoon de snelheid waarmee de kromme wordt getraceerd. Als \(n > 1\) verhogen we de snelheid en als \(n < 1\) verlagen we de snelheid.
laten we nog een paar voorbeelden bekijken.,
tot dit punt hebben we voorbeelden gezien die de volledige grafiek zouden traceren die we kregen door de parameter te elimineren als we een groot genoeg bereik van \(t\)’s namen. echter, in het vorige voorbeeld hebben we nu gezien dat dit niet altijd het geval zal zijn. Het is meer dan mogelijk om een reeks parametrische vergelijkingen te hebben die continu slechts een deel van de curve zullen traceren. We kunnen meestal bepalen of dit zal gebeuren door te zoeken naar limieten op \(x\) en \(y\) die ons worden opgelegd door de parametrische vergelijking.,
We zullen vaak parametrische vergelijkingen gebruiken om het pad van een object of deeltje te beschrijven. Laten we daar een voorbeeld van nemen.
we zouden op dit punt een kleine waarschuwing moeten geven. Vanwege de ideeën die daarbij betrokken waren, hebben we ons geconcentreerd op parametrische krommen die meer dan eens delen van de kromme herleidden. Raak echter niet te verstrikt in het idee dat dit altijd zal gebeuren. Veel, zo niet de meeste parametrische curves zullen slechts één keer worden getraceerd. De eerste die we bekeken is daar een goed voorbeeld van. Die parametrische kromme zal nooit een deel van zichzelf herhalen.,
Er is nog een laatste onderwerp dat in deze sectie besproken moet worden voordat we verder gaan. Tot nu toe zijn we begonnen met parametrische vergelijkingen en de parameter geëlimineerd om de parametrische kromme te bepalen.
echter, er zijn momenten waarop we de andere kant op willen. Gegeven een functie of vergelijking willen we er misschien een set parametrische vergelijkingen voor opschrijven. In deze gevallen zeggen we dat we de functie parametreren.
als we voorbeelden 4 en 5 als voorbeelden nemen kunnen we dit doen voor ellipsen (en dus Cirkels)., Gegeven de ellips
\
een verzameling parametrische vergelijkingen waarvoor het zou zijn,
\
deze verzameling parametrische vergelijkingen zal de ellips traceren vanaf het punt \(\left( {a,0} \right)\) en zal in tegenwijzerzin volgen en exact één keer traceren in het bereik \(0 \le T \le 2\pi \). Dit is een vrij belangrijke verzameling parametrische vergelijkingen zoals het voortdurend gebruikt in sommige onderwerpen met betrekking tot ellipsen en/of Cirkels.
elke curve kan op meer dan één manier worden geparametreerd. Elk van de volgende zal ook dezelfde ellips parametreren.,
\
de aanwezigheid van de \(\omega \) zal de snelheid veranderen die de ellips draait zoals we zagen in Voorbeeld 5. Merk ook op dat de laatste twee ellipsen zullen traceren met een richting van beweging met de klok mee (je zou dit willen verifiëren). Merk ook op dat ze niet allemaal op dezelfde plaats beginnen (als we \(t = 0\) als uitgangspunt beschouwen).
er zijn natuurlijk veel meer parameterisaties van een ellips, maar je snapt het idee. Het is belangrijk om te onthouden dat elke parametrering de kromme eenmaal zal traceren met een potentieel verschillend bereik van \(t\)’s., Elke parametrering kan draaien met verschillende richtingen van beweging en kan beginnen op verschillende punten.
het kan zijn dat je een parametrering nodig hebt van een ellips die begint op een bepaalde plaats en een bepaalde bewegingsrichting heeft.je weet nu dat je met wat werk een set parametrische vergelijkingen kunt opschrijven die je het gedrag geven waar je naar op zoek bent.
laten we nu een paar andere belangrijke parameterisaties opschrijven en alle opmerkingen over bewegingsrichting, startpunt en bereik van \(t\)’s voor één spoor (indien van toepassing) zijn nog steeds waar.,
ten eerste, omdat een cirkel niets meer is dan een speciaal geval van een ellips kunnen we de parametrering van een ellips gebruiken om de parametrische vergelijkingen te krijgen voor een cirkel die gecentreerd is op de oorsprong van straal \(r\). Een mogelijke manier om een cirkel te parametreren is,
\ \
op dit punt lijkt het misschien niet zo nuttig om een parametrering van een functie als deze uit te voeren, maar er zijn veel gevallen waarin het eigenlijk gemakkelijker zal zijn, of het kan zelfs nodig zijn, om te werken met de parametrering in plaats van de functie zelf., Helaas komen bijna al deze gevallen voor in een Calculus III cursus.
















Geef een reactie