mobiele notitie tonen alle notities verbergen alle notities
sectie 4-11 : Lineaire benaderingen
In deze sectie gaan we kijken naar een toepassing Niet van derivaten, maar van de raaklijn aan een functie. Natuurlijk, om de raaklijn te krijgen moeten we derivaten nemen, dus in zekere zin is dit ook een toepassing van derivaten.
\
bekijk de volgende grafiek van een functie en zijn raaklijn.
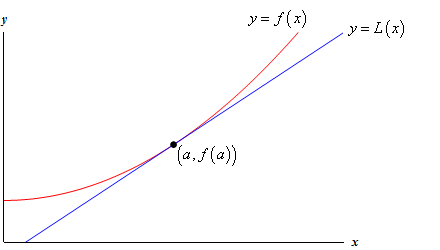
dus, waarom zouden we dit doen? Laten we een voorbeeld nemen.,
Lineaire benaderingen doen zeer goed werk van het benaderen van waarden van \(F \left(x\ right)\) zolang we “dichtbij”\(x = a\) blijven. Echter, hoe verder weg van \(x = A\) we krijgen, hoe slechter de benadering kan zijn. Het grootste probleem hier is dat hoe dicht we bij \(x = a\) moeten blijven om een goede benadering te krijgen, zal afhangen van zowel de functie die we gebruiken als de waarde van \(x = A\) die we gebruiken. Ook zal er vaak geen gemakkelijke manier zijn om te voorspellen hoe ver weg van \(x = A\) We kunnen komen en nog steeds een “goede” benadering hebben.,
laten we eens kijken naar een ander voorbeeld dat eigenlijk vrij zwaar wordt gebruikt op sommige plaatsen.
Dit is eigenlijk een enigszins belangrijke lineaire benadering. In de optica wordt deze lineaire benadering vaak gebruikt om formules te vereenvoudigen. Deze lineaire benadering wordt ook gebruikt om de beweging van een slinger en trillingen in een string te beschrijven.
















Geef een reactie