Black-Scholes Model: eerste stappen
Blog
vandaag bekijken we het meest populaire optieprijsmodel. Het Black Scholes-Model, ook bekend als de Black-Scholes-Merton-methode, is een wiskundig model voor de prijsstelling van optiecontracten. Het werkt door het schatten van de variatie in financiële instrumenten. De techniek berust op de veronderstelling dat de prijzen een lognormale verdeling volgen. Op basis hiervan ontleent het de waarde van een optie.,
Het is geschikter voor padonafhankelijke opties die de beleggers niet vóór hun vervaldatum kunnen uitoefenen. Dit maakt het anders dan het binomiale optieprijsmodel, dat een risiconeutrale methode is voor het waarderen van padafhankelijke opties (bijvoorbeeld Amerikaanse opties).analisten en beleggers beschouwen zwarte Scholes als een van de essentiële concepten in de moderne financiële theorie.het model werd in 1973 geïntroduceerd in het Journal of Political Economy, door Fischer Black en Myron Scholes, en later gebouwd door Robert Merton.,
het model volgt een differentiaalvergelijking, die we gebruiken om de prijzen van opties op te lossen. We gebruiken de standaardvariatie van het model voor Europese stijlopties. Black Scholes is niet geschikt voor Amerikaanse stijl opties, als het niet overwegen beleggers kunnen uitoefenen deze opties op elk moment voor hun vervaldatum.
De methode gaat ervan uit dat de koers van de onderliggende aandelen een lognormale verdeling volgt, aangezien deze niet negatief kan zijn. De verdeling waarop het model zich baseert is gebaseerd op Brownse beweging, een theorie voor het voorspellen van natuurlijk voorkomende willekeurige fenomenen.,
we gebruiken het model om een schatting te berekenen voor de prijs van een optie, aan de hand van de volgende informatie:
- de huidige prijs;
- de uitoefenprijs;
- tijd tot vervaldatum;
- verwachte dividendopbrengst;
- verwachte rente; en
- verwachte volatiliteit.
aanvankelijk houdt het model geen rekening met het effect van dividenduitkeringen. Daarom wordt het vaak aangepast om dit te doen door het bepalen van de ex-dividend datum waarde van het onderliggende actief., Het dividendrendement heeft als gevolg dat de huidige aandelenkoers daalt omdat de optiehouder afstand doet van de dividenden.
aannames
Het Black Scholes-model werkt alleen als we bepaalde aannames maken.,de markten zijn volledig efficiënt, wat betekent dat we hun bewegingen niet kunnen voorspellen;
zwarte Scholes-formule
De modelformule is wiskundig gezien vrij complex, wat geen specifiek probleem is, omdat we gespecialiseerde hulpmiddelen kunnen gebruiken om het voor ons te berekenen. Maar het is nog steeds essentieel om te begrijpen hoe het werkt.,
Voor het berekenen van de prijs van een call optie, onder de Black Scholes-model, kunnen we gebruik maken van de volgende vergelijking:
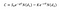
Waar:
- S0 is de koers van het aandeel;
- e is de exponentiële aantal;
- q is het dividend rendement percentage;
- T is de termijn (één jaar worden T=1, terwijl zes maanden zal T=0.,5);
- N(d1) is de delta van de calloptie, wat betekent dat de verandering in de calloptie tijdens de verschuiving in de aandelenkoers;
- K is de uitoefenprijs;
- r is de risicovrije rente; en
- N(d2) is de waarschijnlijkheid dat de toekomstige aandelenkoers hoger zal zijn dan de uitoefenprijs, de waarschijnlijkheid dat we de optie zullen uitoefenen.
één zijde is de aandelenkoers vermenigvuldigd met de cumulatieve standaard normale verdeling van d1, en de andere — de uitoefenprijs, gedisconteerd tot tijd T en vervolgens vermenigvuldigd met de cumulatieve standaard normale verdeling van d2.,
Waar kunnen we berekenen d1 en d2 met de volgende formules:
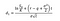
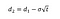
Waar σ de volatiliteit van het rendement van het onderliggende actief.,
Wij kunnen gelden dezelfde logica voor een put optie:
word lid van onze Nieuwsbrief voor een GRATIS Excel-Benchmark Analyse van Sjabloon
Voorbeeld Black Scholes-Berekening
om beter Te illustreren het concept achter de Black Scholes-Model, zullen we een kijkje nemen op het volgende model. We beginnen met de modelinvoer., Zoals hierboven besproken, hebben we de volgende zes variabelen nodig om de call-en putoptiewaarden te berekenen.
volgende, We zullen de parameters van de opties berekenen. Beginnend met d1, krijgen we 0,39 van onze model veronderstellingen.
te berekenen het, we brengen gewoon de formule voor D1 naar Excel.,
Following the same approach, we calculate d2, N(d1) and N(d2).
With those, we can calculate the Call Option Price and the Put Option Price.,
We kan de call-put pariteitsregel gebruiken om te controleren of onze formules en berekeningen correct zijn.
nu we ons model hebben om de call-en putoptieprijzen te berekenen, kunnen we een stap verder gaan en kijken hoe de verschillende inputparameters de resultaten van ons model beïnvloeden., De functionaliteit van de gegevenstabel in Excel is een geweldig hulpmiddel om een aantal gevoeligheidsanalysetabellen voor onze variabelen voor te bereiden. U kunt leren hoe u gegevenstabellen gebruikt in ons artikel gevoeligheidsanalyse.
laten we eens kijken naar de aandelenkoers als deze verandert van €10 naar €100 en hoe het de Call-en Putwaarden beïnvloedt. We merken dat de calloptie geen waarde heeft tot de aandelenkoers €40 bereikt. We zien het omgekeerde voor de putoptie, waar de waarde nul raakt zodra de aandelenkoers boven de €85 komt.,
Als we bereiden dezelfde gevoeligheid tabel voor de Uitoefenprijs, zien we de omgekeerde relatie. Als de staking prijs stijgt, de Call waarde daalt, en de Put waarde gaat omhoog.
laten we ook eens kijken naar de risicovrije rente., Naarmate het stijgt, verhoogt dit ook het vereiste rendement. Vervolgens vermindert dit de waarde van de voorraden. We merken een directe relatie, als de risicovrije rente stijgt, de waarde van de calloptie stijgt ook, terwijl de waarde van de putoptie zijn waarde vermindert.
volgens dezelfde aanpak kunt u verder gaan en kijken naar de rest van de parameters en hoe ze de optiewaarden beïnvloeden., U kunt het Excel-model downloaden aan het einde van het artikel en de gevoeligheidsanalyse daarin doornemen.
u kunt het voorbeeldmodel in Excel downloaden in het oorspronkelijke artikel.
conclusie
Het is belangrijk te onthouden dat het Black-Scholes-Merton-model een theoretisch concept is. We gebruiken het om te proberen het gedrag van de markt in te schatten. Wanneer we de resultaten echter gebruiken in ons besluitvormingsproces, moeten we de onderliggende aannames in het model begrijpen en hoe het afwijkt van de realiteit.,
De formule hielp optiehandel populairder te worden, omdat het minder op gokken lijkt. Tegenwoordig zijn verschillende modificaties van Black Scholes alom populair als fundamentele strategieën voor risicobeheersing, geassocieerd met volatiliteit.
u kunt uw steun tonen door het artikel te delen met collega ‘ s en vrienden.
© 2021 Tombouctou
Thema gemaakt door Anders Noren — Boven ↑
Geef een reactie