Modèle de Black-Scholes: Premiers pas

Aujourd’hui, nous prenons un regard sur les options les plus populaires, le modèle de tarification. Le modèle Black Scholes, également connu sous le nom de méthode Black-Scholes-Merton, est un modèle mathématique pour la tarification des contrats d’option. Il fonctionne en estimant la variation des instruments financiers. La technique repose sur l’hypothèse que les prix suivent une distribution lognormale. Sur cette base, il dérive la valeur d’une option.,

Il est plus approprié pour les options indépendantes du chemin, que les investisseurs ne peuvent pas exercer avant leur date d’échéance. Cela le rend différent du modèle Binomial de tarification des options, qui est une méthode sans risque pour évaluer les options dépendantes du chemin (par exemple, les options américaines).

Les analystes et les investisseurs considèrent Black Scholes comme l’un des concepts essentiels de la théorie financière moderne.

introduit en 1973 dans le Journal of Political Economy, par Fischer Black et Myron Scholes, et plus tard construit sur par Robert Merton, le modèle a remporté le prix Nobel d’économie en 1997.,

le modèle suit une équation différentielle, que nous utilisons pour résoudre les prix des options. Nous utilisons la variante standard du modèle pour les options de style européen. Black Scholes ne convient pas aux options de style américain, car il ne considère pas que les investisseurs peuvent exercer ces options à tout moment avant leur date d’expiration.

la méthode suppose que le cours de l’action sous-jacente suit une distribution lognormale, car il ne peut pas être négatif. La distribution sur laquelle repose le modèle est basée sur le mouvement brownien, une théorie permettant de prédire les phénomènes aléatoires naturels.,

nous utilisons le modèle pour calculer une estimation du prix d’une option, en utilisant les informations suivantes:

• Le prix actuel;
• Le prix d’exercice;
• délai d’expiration;
• rendement du dividende attendu;
• taux D’intérêt attendu; et
• volatilité attendue.

initialement, le modèle ne prend pas en compte l’effet des versements de dividendes. Par conséquent, il est souvent adapté pour le faire en déterminant la valeur à la date ex-dividende de l’actif sous-jacent., Le rendement du dividende a pour effet de réduire le cours actuel de l’action parce que le détenteur de l’option renonce aux dividendes.

hypothèses

le modèle de Black Scholes ne fonctionne que si nous faisons certaines hypothèses.,les options d’achat et de vente n’impliquent aucun coût de transaction;

formule de Black Scholes

la formule du modèle est assez complexe mathématiquement, ce qui n’est pas un problème particulier, car nous pouvons utiliser des outils spécialisés pour la calculer pour nous. Mais il est toujours essentiel de comprendre comment cela fonctionne.,

Pour calculer le prix d’une option d’achat, en vertu du modèle Black Scholes, nous pouvons utiliser l’équation suivante:

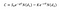
Où:

• S0 est le prix de l’action;
• e est le nombre exponentiel;
• q est le taux de rendement pourcentage;
• T est le terme (une année est T=1, tandis que six mois seront en T=0.,5);
• N (d1) est le delta de l’option d’achat, c’est-à-dire la variation du prix d’appel par rapport à la variation du cours de l’action;
• K est le prix d’exercice;
• r est le taux sans risque; et
• N(d2) est la probabilité que le cours futur de

Un côté est le prix de l’action multiplié par la distribution normale standard cumulative de d1, et l’autre — le prix d’exercice, actualisé au temps T, puis multiplié par la distribution normale standard cumulative de d2.,

Où l’on peut calculer d1 et d2 avec les formules suivantes:

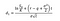
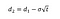
Où σ est la volatilité des rendements de l’actif sous-jacent.,

Nous pouvons appliquer la même logique pour une option de vente:

vous inscrire à notre Newsletter pour GRATUIT Excel de Référence Modèle d’Analyse

Exemple de Black & Scholes Calcul

Pour mieux illustrer le concept derrière le Modèle Black Scholes, nous allons prendre un regard sur le modèle suivant. Nous commençons par les entrées du modèle., Comme discuté ci-dessus, nous avons besoin des six variables suivantes pour calculer les valeurs d’option call et put.

Ensuite, nous allons calculer les options « paramètres ». À partir de d1, nous obtenons 0,39 à partir de nos hypothèses de modèle.

Pour le calculer, il suffit de transfert de la formule de d1 à Excel.,

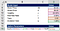
Following the same approach, we calculate d2, N(d1) and N(d2).

With those, we can calculate the Call Option Price and the Put Option Price.,

Nous pouvons employer l’Appel-Mettre de la Parité de la règle pour vérifier si nos formules et les calculs sont corrects.

Maintenant que nous avons notre modèle pour calculer les options Call et Put de prix, nous pouvons aller plus loin et de regarder la façon dont les différents paramètres d’entrée affecter les résultats de notre modèle., La fonctionnalité de table de données dans Excel est un excellent outil pour préparer des tableaux d’analyse de sensibilité pour nos variables. Vous pouvez apprendre à utiliser les tableaux de données dans notre article analyse de sensibilité.

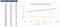
regardons le cours de L’action s’il passe de 10 €à 100 €et comment il affecte les valeurs Call et Put. Nous remarquons que l’Option D’achat n’a aucune valeur jusqu’à ce que le cours de l’action atteigne 40€. Nous voyons l’inverse pour L’Option de vente, où sa valeur atteint zéro une fois que le cours de l’action dépasse 85€.,

Si l’on prépare le même tableau de sensibilité pour le Prix de la Grève, on peut observer la relation inverse. À mesure que le prix d’exercice augmente, la valeur D’appel diminue et la valeur de vente augmente.

nous allons aussi jeter un oeil au risque gratuit taux., À mesure qu’il augmente, cela augmente également le taux de rendement requis. Par la suite, cela diminue la valeur des stocks. Nous remarquons une relation directe, à mesure que le taux sans risque augmente, la valeur de l’Option D’achat augmente également, tandis que la valeur de l’Option de Vente diminue sa valeur.

en Suivant la même approche, vous pouvez aller de l’avant et de regarder le reste des paramètres et comment ils affectent les Valeurs de l’Option., Vous pouvez télécharger le modèle Excel à la fin de l’article et aller sur l’analyse de sensibilité là.

Vous pouvez télécharger l’exemple de modèle dans Excel dans l’article original.

Conclusion

Il est important de se rappeler que le modèle de Black-Scholes-Merton est un concept théorique. Nous l’utilisons pour essayer d’estimer le comportement du marché. Cependant, lorsque nous utilisons les résultats dans notre processus décisionnel, nous devons comprendre les hypothèses sous-jacentes du modèle et comment il s’écarte de la réalité.,

la formule a aidé le trading d’options à devenir plus populaire, car elle le fait ressembler moins au jeu. De nos jours, diverses modifications de Black Scholes sont largement populaires en tant que stratégies fondamentales pour le contrôle des risques, associées à la volatilité.

Vous pouvez montrer votre soutien en partageant l’article avec vos collègues et amis.