Lorsque les Angles d’un Triangle N’atteignent pas 180 degrés

1. Introduction

Les angles d’un triangle ajoutent-ils jusqu’à 180 degrés ou radi\pi radi radians? La réponse est « parfois oui, parfois non ». Est-ce une question importante? Oui, car cela conduit à comprendre qu’il existe différentes géométries basées sur différents axiomes ou « règles du jeu de la géométrie ». Est-ce une question significative? Eh bien non, du moins pas avant que nous nous soyons mis d’accord sur la signification des mots « angle » et « angle », pas avant que nous connaissions les règles du jeu., Dans cet article, nous discuterons brièvement les axiomes sous-jacents et de donner une preuve simple que la somme des angles d’un triangle sur la surface d’une sphère unité n’est pas égal à $\pi$ mais $\pi$ plus l’aire du triangle. Nous utiliserons le fait que l’aire de la surface d’une sphère unitaire est $4\pi pi.

2. Le Grand théorème

avant de pouvoir dire ce qu’est un triangle, nous devons nous mettre d’accord sur ce que nous entendons par points et lignes. Nous travaillons sur la géométrie sphérique (littéralement géométrie à la surface d’une sphère)., Dans cette géométrie, l’espace est la surface de la sphère; les points sont des points sur cette surface, et la ligne de distance la plus courte entre deux points est le grand cercle contenant les deux points. Un grand cercle (commel’Équateur) coupe la sphère en deux hémisphères égaux. Cette géométrie a des applications évidentes aux distances entre les endroits et les routes aériennes sur la Terre.,

Rotation de la sphère montrant un grand cercle

L’angle entre les deux grands cercles en un point P est le Euclidienne angle entre les directions des cercles (ou strictement entre les tangentes aux cercles à P). Cela ne présente aucune difficulté dans la navigation sur la terre parce qu’à un point donné, nous pensons à l’angle entre deux directions comme si la Terre était plate à ce point.

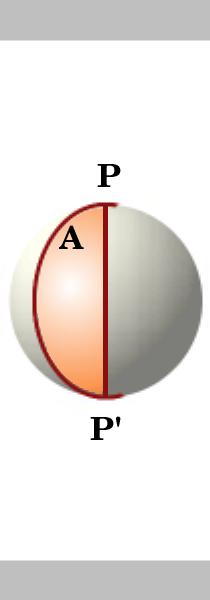
une lune est une partie de la surface de la sphère délimitée par deux grands cercles qui se rencontrent aux points antipodaux., Nous considérons d’abord l’aire d’une lune, puis introduisons un autre grand cercle qui divise la lune en triangles.

Rotation de la sphère montrant des 4 lunes

Lemme.

l’aire d’une lune sur un cercle de rayon unitaire est deux fois son angle, c’est-à-dire si l’angle de la lune est A alors son aire est 2A. deux grands cercles se croisant aux points antipodaux P et P’ divisent la sphère en 4 lunes. L’aire de la surface d’une sphère unitaire est $4\pi pi.,

Les aires des lunes sont proportionnelles à leurs angles à P donc l’aire d’une lune avec l’angle A est

{{\frac{a} {2\pi}\times {4\pi}= {2a}} Exercise

Exercice 1.

quelles sont les zones des 3 autres lunes? Est-ce que vos 4 zones ajoutent jusqu’à 4 4 \ pi??

vérifie tes réponses ici .

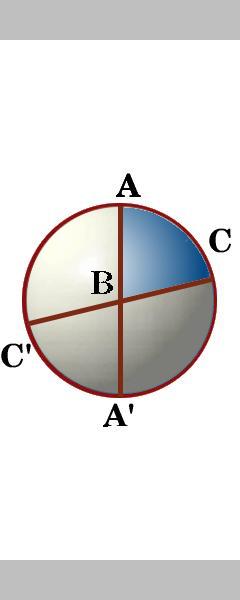
les côtés D’un triangle ABC sont des segments de trois grands cercles qui coupent en fait la surface de la sphère en huit triangles sphériques. Entre les deux grands cercles à travers le point A, Il y a quatre angles., Nous étiquetons l’angle à l’intérieur du triangle ABC comme angle A, et de même les autres angles du triangle ABC comme angle B et angle C.

sphère rotative montrant 8 triangles

Exercice 2

rotation de la sphère pouvez-vous nommer les huit triangles et dire si l’un d’eux a la même surface? Vérifiez vos réponses ici .

théorème.

considérons un triangle sphérique ABC sur la sphère unité avec les angles A, B et C. Alors l’aire du triangle ABC est

A + B + C – \ \ pi pi.,

Le diagramme montre une vue regardant vers le bas sur l’hémisphère qui a la ligne à travers AC comme limite. Les régions marquées Zone 1 et Zone 3 sont des lunes avec des angles A et c respectivement. Considérez les lunes à travers B et B’. Le Triangle ABC est congru au triangle A’B’C’ de sorte que la zone ombrée en forme de nœud papillon, marquée Zone 2, qui est la somme des aires des triangles ABC et A’BC’, est égale à la zone de la lune avec l’angle B, qui est égal à 2B.,

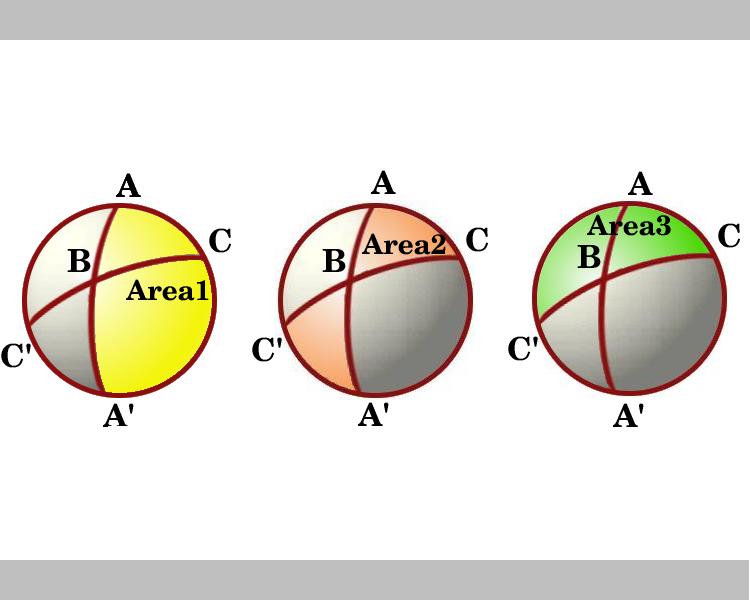
Ainsi, dans le diagramme, nous voyons les domaines des trois lunes et, en utilisant le lemme, ce sont:

Zone 1 = 2A
Zone 2 = 2B
Zone 3 = 2C

En additionnant ces trois domaines, nous incluons l’aire du triangle ABC trois fois., Hence

3., Géométrie non euclidienne

parfois, les découvertes révolutionnaires ne sont rien de plus que de voir ce qui a été sous notre nez tout le temps. Ce fut le cas lors de la découverte de la géométrie non euclidienne au XIXe siècle. Pendant environ 2000 ans après Euclide a écrit ses « éléments » en 325 avant JC, les gens ont essayé de prouver le postulat parallèle comme un théorème dans la géométrie des autres axiomes, mais a toujours échoué et c’est une longue histoire., Pendant ce temps, les mathématiciens utilisaient la géométrie sphérique tout le temps, une géométrie qui obéit aux autres axiomes de la géométrie euclidienne et contient plusieurs des mêmes théorèmes, mais dans laquelle le postulat parallèle ne tient pas. Tout au long, ils avaient un exemple de géométrie non euclidienne sous le nez.

pensez à une ligne L et à un point P non sur L. La grande question Est: « combien de lignes peuvent être tracées à travers P parallèlement à L? »En géométrie euclidienne, la réponse est `exactement un » et c’est une version du postulat parallèle., Si la somme des angles de chaque triangle de la géométrie est $\pi radi radians alors le postulat parallèle est valable et vice versa, les deux propriétés sont équivalentes.

En géométrie sphérique, les axiomes de base que nous supposons (les règles du jeu) sont différents de la géométrie euclidienne – c’est une géométrie Non euclidienne. Nous avons vu qu’en géométrie sphérique, les angles des triangles ne s’additionnent pas toujours à radi \ pi radi radians, donc nous ne nous attendrions pas à ce que le postulat parallèle tienne., En géométrie sphérique, les lignes droites (lignes de la plus courte distance ou géodésiques)sont de grands cercles et chaque ligne de la géométrie coupe toutes les autres lignes en deux points. La réponse à la Grande question sur les parallèles est`si nous avons une ligne L et un point P non sur L, il N’y a pas de lignes passant par P parallèlement à la ligne L., »

les mathématiciens Grecs (par exemple Ptolémée vers 150) ont calculé les mesures des triangles sphériques à angle droit et ont travaillé avec des formules de trigonométrie sphérique et les mathématiciens Arabes (Par exemple Jabir ibn Aflah vers 1125 et Nasir ed-din vers 1250) ont étendu le travail encore plus loin. La formule discutée dans cet article a été découverte par Harriot en 1603 et publiée par Girard en 1629. D’autres idées du sujet ont été développées par Saccerhi (1667 – 1733).,

tout cela a été largement non remarqué par les découvreurs du 19ème siècle de la géométrie hyperbolique, qui est une autre géométrie non euclidienne où le postulat parallèle ne tient pas. En géométrie sphérique (également appelée géométrie elliptique) les angles des triangles ajouter jusqu’à plus de $\pi$ radians et en géométrie hyperbolique les angles des triangles ajouter jusqu’à moins de $\pi$ radians.

pour en savoir plus, voir L’article D’Alan Beardon  » Combien y a-t-il de géométries? »et L’article de Keith Carne « géométries étranges »., Il y a quelques activités pratiques que vous pouvez essayer vous-même pour explorer ces géométries plus loin à http://nrich.maths.org/MOTIVATE/conf8/index.html