un nombre pair est un entier qui peut être divisé exactement ou uniformément par \color{red}2. Si un nombre est exactement divisé par \color {red} 2, cela implique que le nombre en question a un reste de \color{blue}0 sur la division de \color{red}2.
en effectuant des mathématiques mentales, il est évident que les nombres ci-dessous, y compris les nombres négatifs, sont pairs parce qu’ils sont tous divisibles par 2.,

En outre, je tiens à souligner que de nombreux étudiants pensent zéro est ni le même ni impair.
Croyez-moi, zéro est considéré comme un nombre pair pour la même raison simple que c’est aussi un nombre entier est divisible par 2 donc pas de reste quand divisé par 2 ainsi. Autrement dit, 0 \div 2 = 0.
Observation: à partir des exemples ci-dessus, nous pouvons facilement généraliser que les nombres pairs se terminent toujours par un chiffre de 0, 2, 4, 6 ou 8.,
Cependant, il existe une meilleure façon de définir un nombre pair, car il est plus mathématiquement précis. Ici il est!
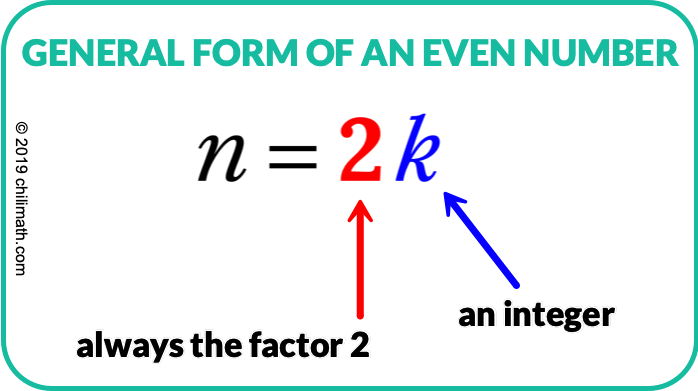
la Forme Générale d’un Nombre pair
des Exemples de Même des Nombres Exprimés dans la Forme Générale
Mettons la forme générale d’un même nombre à l’épreuve. Quel que soit le concept mathématique qui nous est présenté, il est crucial que nous le vérifiions. Cela devrait en quelque sorte avoir du sens pour nous avant de l’inclure dans notre « math toolbox”.,
Voici quelques exemples pour présenter le concept d’un nombre pair comme n = 2\,k où k est un entier.
\color{red}\LARGE {n = 2k}
- 0 \0 = 2\left( 0 \right)
- 14 \14 = 2\left( 7 \right)
- – 32 \à – 32 = 2\left( { – 16} \right)
- 50 \50 = 2\left( {25} \right)
- – 78 \à – 78 = 2\left( { – 39} \right)
L’apparition constante de 2 comme l’un des facteurs d’un nombre pair suggère que tous les nombres pairs sont en effet un multiple de 2.,
Vous pourriez également être intéressé par:
Ce qui est un nombre impair?
Liste des Nombres
Liste des Numéros Impairs
















Laisser un commentaire