les Hommes. Je sens, en quelque sorte, que j’aime ce que vous dites.
Soc. Et moi, Meno, j’aime ce que je dis.
à partir de Platon, Ménon
la longueur de La diagonale du carré de l’unité est égale à la racine carrée de 2.
la longueur de la diagonale du carré unitaire est égale à √2. Eh bien, ce n’est pas vraiment une bonne nouvelle. Tous ceux qui sont tombés sur le théorème de Pythagore sont conscients du fait., Dans le triangle rectangle isocèle avec les jambes de longueur 1, l’hypoténuse, selon le théorème de Pythagore – 12 + 12 = (hypoténuse)2 – est en effet de longueur √2. La motivation de cette page n’est pas tant ce fait lui-même, mais la façon de le montrer sans recourir au fameux théorème. En effet, on pourrait soutenir que le théorème de Pythagore aurait pu être surutilisé, voir un exemple curieux.
un argument qui remonte à la figure dessinée par Socrate dans le Ménon de Platon aurait pu être connu de Pythagore lui-même, bien que ce dernier ait vécu un siècle plus tôt.,
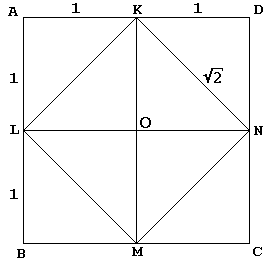
dans le dialogue, Socrate, à sa manière habituelle, conduit un jeune esclave à une construction d’un carré deux fois l’aire de celui donné:
Le Carré klmn donné de Centre O est d’abord coupé par ses diagonales en 4 triangles égaux. Socrate intègre KLMN dans un plus grand carré ABCD comme s’il reflétait ces triangles chacun dans son hypoténuse. L’esclave admet alors-et qui ne le ferait pas? – ce carré ABCD est deux fois plus grand que le carré KLMN.
à vrai dire, le carré ABCD de Socrate mesurait 4 sur le côté, de sorte que le carré KLMN avait une aire de 8., Il est clair que lorsque nous commençons par le carré ABCD de côté 2 (et donc d’aire 4), Le Carré KLMN aura l’aire de 2.
Maintenant, en général, pour un nombre positif A, √A est défini comme un nombre dont le carré est Un:
(√A)2.
d’autre part, chaque élève d’areas sait que l’aire d’un carré de côté b est égale à b2. Il s’ensuit alors que le côté d’un carré d’aire A est exactement √A. Nous concluons que le côté du carré KLMN est égal à √2. Pour l’un,
KN = √A.
Le point central de l’argument est le fait que, dans le diagramme, KN joue un double rôle., En plus d’être l’un des côtés du carré KLMN, il sert également de diagonale du carré OKDN. Ce dernier est bien sûr un carré d’Unité, ce qui prouve notre affirmation.
(D’un point de vue un peu différent, le même épisode est mentionné ailleurs.)
















Laisser un commentaire