これまでに説明したアンプのタイプは、オーディオ周波数に優れていても、無線周波数で効果的に動作することはできません。 また、これらの増幅器の利得は、広い範囲にわたって、信号の周波数に応じて変化しないようなものである。, これは、周波数の範囲にわたって同様に良好に信号の増幅を可能にし、他の周波数を拒絶しながら、特定の所望の周波数の選択を可能にしない。したがって、増幅だけでなく選択できる回路が必要になります。 したがって、同調回路のような選択とともに増幅回路が同調増幅器を作る。
チューニングアンプとは何ですか?
チューニングアンプは、チューニングの目的で使用されるアンプです。 チューニング手段を選択す., 利用可能な周波数のセットの中で、特定の周波数を選択する必要が生じた場合、他のすべての周波数を拒否しながら、そのようなプロセスは選択と呼 この選択は、同調回路と呼ばれる回路を使用して行われます。
増幅回路の負荷が同調回路に置き換えられている場合、このような増幅器を同調増幅回路と呼ぶことができる。 基本的なチューニングアンプ回路は以下のようになります。
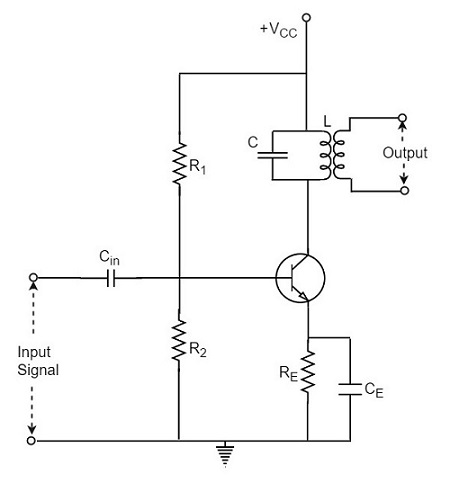
チューナ回路は、共振回路またはタンク回路とも呼ばれるLC回路に過ぎません。 これは、周波数を選択します。, 同調回路は、共振周波数を中心とする狭帯域の周波数にわたって信号を増幅することができる。
インダクタのリアクタンスがコンデンサのリアクタンスとバランスをとると、ある周波数の同調回路では、そのような周波数を共振周波数と呼ぶことができます。 それはfrで表されます。,
共振の式は
$$2\pi f_L=\frac{1}{2\pi f_c}$$
$$f_r=\frac{1}{2\pi\sqrt{LC}}$$
同調回路の種類
同調回路は、メインとの接続のタイプに応じて、直列同調回路(直列共振回路)または並列同調回路(並列共振回路)サーキット
直列同調回路
インダクタとコンデンサを直列に接続すると、次の回路図に示すように直列同調回路が形成されます。,

共振周波数では、直列共振回路は低インピーダンスを提供し、それを通る大電流を可能にします。 直列共振回路は、共振周波数から遠い周波数に対してますます高インピーダンスを提供します。
並列同調回路
インダクタとコンデンサを並列に接続して、下の図のように並列同調回路を作ります。
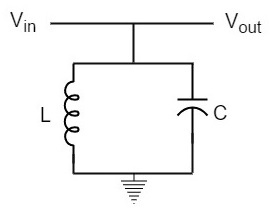
共振周波数では、並列共振回路は高インピーダンスを提供し、それを通る大電流を許容しません。, 並列共振回路は、共振周波数から遠い周波数に対してますます低いインピーダンスを提供します。
並列同調回路の特性
並列共振が起こる周波数(すなわち回路電流の反応成分がゼロになる周波数)を共振周波数frと呼びます。 同調回路の主な特徴は次のとおりです。
インピーダンス
ライン電流に対する電源電圧の比は、同調回路のインピーダンスです。, LC回路によって提供されるインピーダンスは、
$$\frac{Supply\:voltage}{Line equation}=\frac{V}{I}$$
共振時には、インピーダンスが減少しながら線路電流が増加します。
下の図は、並列共振回路のインピーダンス曲線を表しています。
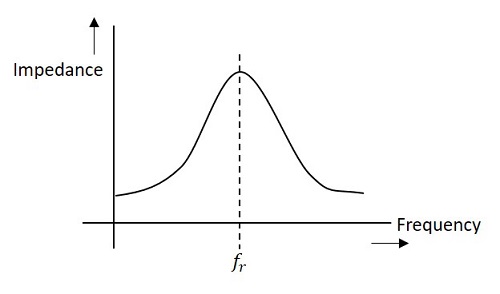
回路のインピーダンスは、共振周波数frの上下の値に対して減少します。 したがって、特定の周波数の選択および他の周波数の除去が可能である。,
To obtain an equation for the circuit impedance, let us consider
Line Current $I = I_L cos \phi$
$$\frac{V}{Z_r} = \frac{V}{Z_L} \times \frac{R}{Z_L}$$
$$\frac{1}{Z_r} = \frac{R}{Z_L^2}$$
$$\frac{1}{Z_r} = \frac{R}{L/C} = \frac{C R}{L}$$
Since, $Z_L^2 = \frac{L}{C}$
Therefore, circuit impedance Zr is obtained as
$$Z_R = \frac{L}{C R}$$
Thus at parallel resonance, the circuit impedance is equal to L/CR.,
回路電流
並列共振では、回路またはライン電流Iは、回路インピーダンスZrで割った印加電圧によって与えられます。
ライン電流$I=\frac{V}{Z_r}$
ここで、$Z_r=\frac{L}{C R}$
なぜなら、ここで$Z_r=\frac{L}{C R}$
zrは非常に高く、ライン電流は非常に小さくなります。
品質係数
並列共振回路の場合、共振曲線の鋭さによって選択性が決定されます。 コイルの抵抗が小さいほど、共振曲線はより鋭くなります。, したがって、コイルの誘導リアクタンスと抵抗によって、同調回路の品質が決まります。
共振時のコイルの抵抗に対する誘導リアクタンスの比は、品質係数として知られています。 これはQで表されます。
$Q=\frac{X_L}{R}=\frac{2\pi f_r L}{R}$
Qの値が高いほど、共振曲線が鋭くなり、選択性が良くなります。
同調アンプのメリット
同調アンプのメリットは次のとおりです。,
-
LやCのようなリアクティブ部品を使用すると、電力損失が最小限に抑えられ、調整されたアンプが効率的になります。
-
共振周波数でより高いインピーダンスを提供することにより、所望の周波数の選択性および増幅が高くなる。
-
並列同調回路では抵抗が少ないため、コレクタ電源VCCが小さくなります。
これらの利点は、高い抵抗コレクタ負荷がある場合には適用できないことを覚えておくことが重要です。,
同調アンプの周波数応答
アンプを効率的にするには、そのゲインが高くなければなりません。 この電圧利得はβ,入力インピーダンス,コレクタ負荷に依存する。 同調アンプのコレクタ負荷は、同調回路です。
このようなアンプの電圧利得は、
電圧利得=$\frac{\beta Z_C}{Z_{in}}$
ここで、ZC=実効コレクタ負荷、zin=アンプの入力インピーダンスです。
ZCの値は、調整されたアンプの周波数に依存します。, ZCは共振周波数で最大であるため、アンプのゲインはこの共振周波数で最大になります。
Bandwidth
同調アンプの電圧利得が最大利得の70.7%に低下する周波数の範囲を帯域幅と呼びます。
f1とf2の間の周波数範囲は、同調アンプの帯域幅と呼ばれます。 同調アンプの帯域幅は、LC回路のQ、すなわち周波数応答の鋭さに依存する。 Qの値と帯域幅は反比例します。,
下の図は、同調アンプの帯域幅と周波数応答を詳細に示しています。
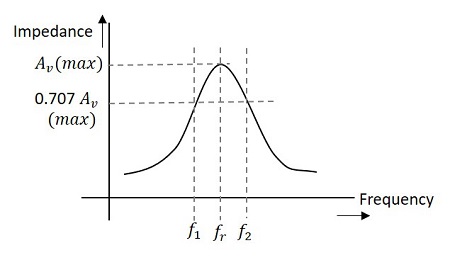
Qと帯域幅の関係
帯域幅の品質係数Qは、帯域幅に対する共振周波数の比として定義されます。
$Q=\frac{f_r}{BW}$
一般に、実用的な回路はQ値が10より大きい。,
この条件下では、並列共振時の共振周波数は
$f_r=\frac{1}{2\pi\sqrt{LC}}$
<
















コメントを残す