Quando gli angoli di un triangolo non sommano fino a 180 gradi

1. Introduzione

Gli angoli di un triangolo si sommano a 180 gradi o radi\pi radi radianti? La risposta è “a volte sì, a volte no”. È una domanda importante? Sì, perché porta a capire che esistono geometrie diverse basate su assiomi diversi o “regole del gioco della geometria”. È una domanda significativa? Beh no, almeno non finché non avremo concordato il significato delle parole “angolo” e “triangolo”, non finché non conosceremo le regole del gioco., In questo articolo discutiamo brevemente gli assiomi sottostanti e diamo una semplice prova che la somma degli angoli di un triangolo sulla superficie di una sfera unitaria non è uguale a \\pi $ma a$ \ pi plus più l’area del triangolo. Useremo il fatto che l’area della superficie di una sfera unitaria è 4 4\pi$.

2. Il grande Teorema

Prima di poter dire cos’è un triangolo dobbiamo essere d’accordo su cosa intendiamo per punti e linee. Stiamo lavorando sulla geometria sferica (letteralmente geometria sulla superficie di una sfera)., In questa geometria lo spazio è la superficie della sfera; i punti sono punti su quella superficie, e la linea di distanza più breve tra due punti è il grande cerchio contenente i due punti. Un grande cerchio (comel’equatore) taglia la sfera in due emisferi uguali. Questa geometria ha ovvie applicazioni alle distanze tra i luoghi e le rotte aeree sulla Terra.,

Sfera rotante che mostra un grande cerchio

L’angolo tra due grandi cerchi in un punto P è l’angolo euclideo tra le direzioni dei cerchi (o strettamente tra le tangenti ai cerchi in P). Questo non presenta difficoltà nella navigazione sulla Terra perché in un dato punto pensiamo all’angolo tra due direzioni come se la Terra fosse piatta in quel punto.

Una lune è una parte della superficie della sfera delimitata da due grandi cerchi che si incontrano in punti antipodali., Consideriamo prima l’area di una lune e poi introduciamo un altro grande cerchio che divide la lune in triangoli.

Sfera rotante che mostra 4 lune

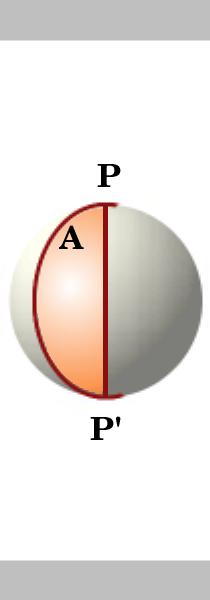
Lemma.

L’area di una lune su un cerchio di raggio unitario è il doppio del suo angolo, cioè se l’angolo della lune è A allora la sua area è 2A. Due grandi cerchi che si intersecano nei punti antipodali P e P’ dividono la sfera in 4 lune. L’area della superficie di una sfera unitaria è 4 4 \ pi$.,

Le aree delle lune sono proporzionali ai loro angoli a P quindi l’area di una lune con angolo A è

{{\frac{A} {2\pi}\times {4\pi}= {2A}} Exercise

Esercizio 1.

Quali sono le aree degli altri 3 lune? Le tue 4 aree aggiungono fino a 4 4 \ pi$?

Controlla le tue risposte qui .

I lati di un triangolo ABC sono segmenti di tre grandi cerchi che in realtà tagliano la superficie della sfera in otto triangoli sferici. Tra i due grandi cerchi attraverso il punto A ci sono quattro angoli., Siamo in etichetta l’angolo interno del triangolo ABC come Un angolo, e allo stesso modo gli altri angoli del triangolo ABC come l’angolo B e angolo C.

ruotare la sfera mostrando di 8 triangoli

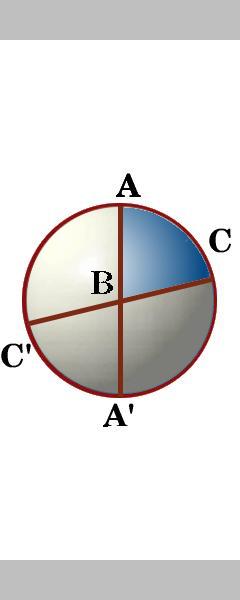
Esercizio 2

Ruotare la sfera può fare il nome di otto triangoli e dire se qualcuno di loro hanno la stessa area? Controlla le tue risposte qui .

Teorema.

Considera un triangolo sferico ABC sulla sfera unitaria con angoli A, B e C. Quindi l’area del triangolo ABC è

A + B + C – \ \ pi$.,

Il diagramma mostra una vista che guarda verso il basso sull’emisfero che ha la linea attraverso AC come confine. Le regioni contrassegnate Area 1 e Area 3 sono lunes con angoli A e C rispettivamente. Considera i lunes attraverso B e B’. Il triangolo ABC è congruente al triangolo A’B’C ‘quindi l’area ombreggiata a forma di papillon, contrassegnata dall’Area 2, che è la somma delle aree dei triangoli ABC e A’BC’, è uguale all’area della luna con angolo B, che è uguale a 2B.,

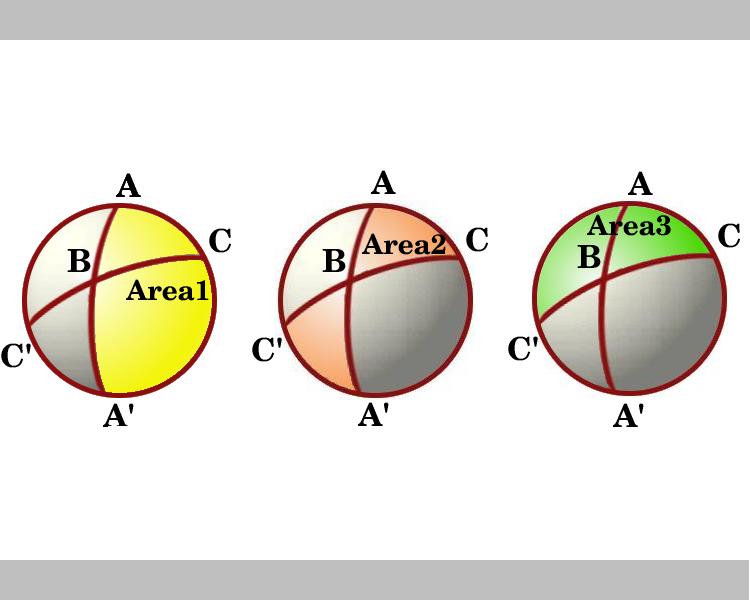
nel diagramma vediamo le aree dei tre lunes e, usando il lemma, questi sono:

Area 1 = 2A
Area 2 = 2B
Area 3 = 2C

In aggiunta a queste tre aree, l’area del triangolo ABC tre volte., Hence

3., Geometria non euclidea

A volte le scoperte rivoluzionarie non sono altro che vedere ciò che è stato sotto il nostro naso tutto il tempo. Questo è stato il caso della scoperta della geometria non euclidea nel diciannovesimo secolo. Per circa 2000 anni dopo che Euclide scrisse i suoi “Elementi” nel 325 AC, la gente cercò di dimostrare il postulato parallelo come teorema nella geometria dagli altri assiomi, ma fallì sempre e questa è una lunga storia., Nel frattempo i matematici stavano usando la geometria sferica per tutto il tempo, una geometria che obbedisce agli altri assiomi della geometria euclidea e contiene molti degli stessi teoremi, ma in cui il postulato parallelo non regge. Per tutto il tempo avevano un esempio di una geometria non euclidea sotto il naso.

Pensa a una linea L e un punto P non su L. La grande domanda è: “Quante linee possono essere disegnate attraverso P parallele a L?”Nella geometria euclidea la risposta è” esattamente una ” e questa è una versione del postulato parallelo., Se la somma degli angoli di ogni triangolo nella geometria è radi\pi radi radianti allora il postulato parallelo tiene e viceversa, le due proprietà sono equivalenti.

Nella geometria sferica, gli assiomi di base che assumiamo (le regole del gioco) sono diversi dalla geometria euclidea – questa è una geometria non euclidea. Abbiamo visto che nella geometria sferica gli angoli dei triangoli non sempre si sommano ai radianti \ \ pi so quindi non ci aspetteremmo che il postulato parallelo reggesse., Nella geometria sferica, le linee rette (linee di distanza più breve o geodetica)sono grandi cerchi e ogni linea nella geometria taglia ogni altra linea in due punti. La risposta alla grande domanda sui paralleli è ” Se abbiamo una linea L e un punto P non su L, allora non ci sono linee attraverso P parallele alla linea L.,”

I matematici greci (ad esempio Tolomeo c 150) calcolarono le misure di triangoli sferici ad angolo retto e lavorarono con formule di trigonometria sferica e matematici arabi (ad esempio Jabir ibn Aflah c 1125 e Nasir ed-din c 1250) ampliarono ulteriormente il lavoro. La formula discussa in questo articolo fu scoperta da Harriot nel 1603 e pubblicata da Girard nel 1629. Furtherideas del soggetto sono stati sviluppati da Saccerhi (1667 – 1733).,

Tutto ciò è andato in gran parte inosservato dagli scopritori del 19 ° secolo della geometria iperbolica, che è un’altra geometria non euclidea in cui il postulato parallelo non regge. Nella geometria sferica (detta anche geometria ellittica) gli angoli dei triangoli si sommano a più di radi\pi radi radianti e nella geometria iperbolica gli angoli dei triangoli si sommano a meno di radi\pi radi radianti.

Per ulteriori approfondimenti si veda l’articolo di Alan Beardon ‘ Quante geometrie ci sono?’e l’articolo di Keith Carne ‘Strane geometrie’., Ci sono alcune attività pratiche che puoi provare per te stesso per esplorare ulteriormente queste geometrie che puoi trovare su http://nrich.maths.org/MOTIVATE/conf8/index.html