Un vettore ha grandezza (quanto tempo è) e direzione:

Qui ci sono due vettori:

Possono essere moltiplicati usando il “Prodotto Dot” (vedi anche Cross Product).,
Siamo in grado di calcolare il Prodotto di Puntino di due vettori in questo modo:

a · b = |a| × |b| x cos(θ)
Dove:
|a| è l’ordine di grandezza (lunghezza) di vector
|b| è l’ordine di grandezza (lunghezza) del vettore b
q è l’angolo tra a e b
Così abbiamo moltiplicare la lunghezza volte la lunghezza di b, quindi moltiplicare per il coseno dell’angolo tra a e b
O si può calcolare in questo modo:
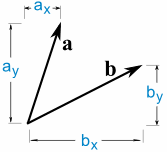
a · b = ax × bx + ay ×
Così si moltiplica la x, per moltiplicare la y, quindi aggiungere.,
Entrambi i metodi funzionano!
E il risultato è un numero (chiamato “scalare” quindi sappiamo che non è un vettore).
Nota: puoi usare il Vettore Calculatorto per aiutarti.
Perché cos (θ)?
OK, per moltiplicare due vettori ha senso moltiplicare le loro lunghezze insieme ma solo quando puntano nella stessa direzione.,
Così facciamo un “punto nella stessa direzione” come le altre moltiplicando cos(θ):
 |
 |
|
| Prendiamo il componente di una che si trova a fianco di b |
Come di una luce brillante per vedere dove si trova l’ombra |
POI si moltiplica !,
Angoli retti
Quando due vettori sono ad angolo retto l’uno rispetto all’altro, il prodotto punto è zero.
Questo può essere un modo pratico per scoprire se due vettori sono ad angolo retto.
Tre o più dimensioni
Tutto questo funziona bene anche in 3 (o più) dimensioni.
E può effettivamente essere molto utile!
Ho provato un calcolo del genere una volta, ma ho lavorato tutto in angoli e distanze … e ‘ stato molto difficile, ha coinvolto un sacco di trigonometria, e il mio cervello male. Il metodo sopra è molto più semplice.,
Cross Product
Il prodotto Dot fornisce una risposta scalare (numero ordinario) ed è talvolta chiamato prodotto scalare.
Ma c’è anche il Prodotto incrociato che dà un vettore come risposta, ed è talvolta chiamato il prodotto vettoriale.
















Lascia un commento