Probabilità che tirando due dadi a sei facce dotssuch come 1, 2, 3, 4, 5 e 6 punti in ogni stampo.

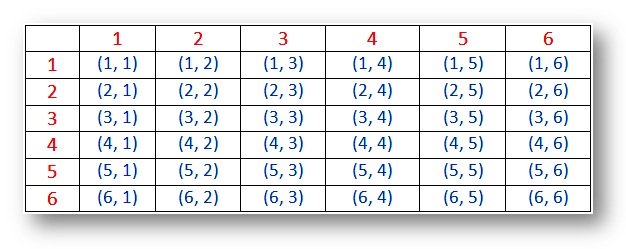
Quando due dadi vengono lanciati contemporaneamente, quindi il numero di eventi può essere 62 = 36 perché ogni dado ha da 1 a 6 numeri sulle sue facce. Quindi i possibili risultati sono mostrati nella tabella sottostante.,
Probabilità – Esempio di spazio per due dadi (esiti):
Nota:
(i) I risultati (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) e (6, 6) sono chiamati doppiette.
(ii) La coppia (1, 2) e (2, 1) sono risultati diversi.
Problemi risolti che coinvolgono probabilità per tirare due dadi:
1. Due dadi sono rotolati. Sia A, B, C gli eventi di ottenere una somma di 2, una somma di 3 e una somma di 4 rispettivamente., Quindi, dimostrare che
(i) A è un semplice evento
(ii) B e C sono composti eventi
(iii) A e B sono mutuamente esclusivi
Soluzione:
Chiaramente, abbiamo
A = {(1, 1)}, B = {(1, 2), (2, 1)} e C = {(1, 3), (3, 1), (2, 2)}.
(i) Poiché A è costituito da un singolo punto di campionamento, è un evento semplice.
(ii) Poiché sia B che C contengono più di un punto campione, ognuno di essi è un evento composto.
(iii) Poiché A B B = ∅, A e B si escludono a vicenda.
2. Due dadi sono rotolati., A è l’evento che la somma dei numeri indicati sui due dadi è 5, e B è l’evento che almeno uno dei dadi mostra un 3.
I due eventi (i) si escludono a vicenda, (ii) sono esaustivi? Fornisci argomenti a sostegno della tua risposta.
Soluzione:
Quando due dadi sono rotolati, abbiamo n (S) = (6 × 6) = 36.
Ora, Un = {(1, 4), (2, 3), (4, 1), (3, 2)}, e
B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}
(i) A ∩ B = {(2, 3), (3, 2)} ≠ ∅.
Quindi, A e B non si escludono a vicenda.,
(ii) Inoltre, A B B S S.
Pertanto, A e B non sono eventi esaustivi.
Altri esempi relativi alle domande sulle probabilità di lanciare due dadi.
3. Due dadi vengono lanciati contemporaneamente.,) ottenendo un doppietto
(v) per ottenere una somma di 8
(vi) come somma divisibile per 5
(vii) di ottenere una somma di almeno 11
(viii) ottenere un multiplo di 3 come somma
(ix) ottenere un totale di almeno 10
(x) per ottenere un numero pari alla somma
(xi) per ottenere un numero primo come somma
(xii) ottenendo un doppietto di numeri
(xiii) ottenere un multiplo di 2, su un dado e un multiplo di 3 su gli altri muoiono
Soluzione:
Due diversi dadi sono gettati contemporaneamente essere il numero 1, 2, 3, 4, 5 e 6 sui loro volti., Sappiamo che in un singolo lancio di due dadi diversi, il numero totale di risultati possibili è (6 × 6) = 36.
(i) ottenere sei come prodotto:
Lascia E1 = evento di ottenere sei come prodotto. Il numero il cui prodotto è sei sarà E1 = = 4
Pertanto, probabilità di ottenere ‘sei come prodotto’
Numero di risultati favorevoli
P(E1) = Numero totale di possibili risultati
= 4/36
= 1/9
(ii) ottenere somma ≤ 3:
Lasciare E2 = evento di ottenere somma ≤ 3., Il numero la cui somma ≤ 3 sarà E2 = = 3
Pertanto, probabilità di ottenere ‘sum ≤ 3’
Numero di risultati favorevoli
P(E2) = Numero totale di possibili risultati
= 3/36
= 1/12
(iii) ottenere sum ≤ 10:
Sia E3 = evento di ottenere sum ≤ 10. Il numero la cui somma ≤ 10 sarà E3 =
= 33
Quindi, probabilità di ottenere ‘sum ≤ 10’
Numero di risultati favorevoli
P(E3)= Numero totale di possibili risultati
= 33/36
= 11/12
(iv)ottenere un doppietto:sia E4 = evento di ottenere un doppietto., Il numero che doublet sarà E4 = = 6
Quindi, probabilità di ottenere ‘un doublet’
Numero di risultati favorevoli
P(E4) = Numero totale di possibili risultati
= 6/36
= 1/6
(v)ottenere una somma di 8:
Sia E5 = evento di ottenere una somma di 8. Il numero che è una somma di 8 sarà E5 = = 5
Pertanto, probabilità di ottenere ‘una somma di 8 ‘
Numero di risultati favorevoli
P (E5)= Numero totale di possibili risultati
= 5/36
(vi) ottenere somma divisibile per 5:
Sia E6 = evento di ottenere somma divisibile per 5., Il numero la cui somma divisibile per 5 sarà E6 = = 7
Pertanto, probabilità di ottenere ‘somma divisibile per 5’
Numero di risultati favorevoli
P (E6)= Numero totale di possibili risultati
= 7/36
(vii) ottenere somma di almeno 11:
Sia E7 = evento di ottenere somma di almeno 11. Gli eventi della somma di almeno 11 saranno E7 = = 3
Pertanto, probabilità di ottenere ‘somma di almeno 11’
Numero di risultati favorevoli
P(E7) = Numero totale di possibili risultati
= 3/36
= 1/12
(viii) ottenere un multiplo di 3 come somma:
Sia E8 = evento di ottenere un multiplo di 3 come somma., Gli eventi di un multiplo di 3 come somma saranno E8 = = 12
Pertanto, probabilità di ottenere ‘un multiplo di 3 come somma’
Numero di risultati favorevoli
P(E8)= Numero totale di possibili risultati
= 12/36
= 1/3
(ix) ottenere un totalof almeno 10:
Sia E9 = evento di ottenere un totale di almeno 10., Gli eventi di un totale di almeno 10 saranno E9 = = 6
Pertanto, probabilità di ottenere ‘un totale di almeno 10’
Numero di risultati favorevoli
P(E9) = Numero totale di possibili risultati
= 6/36
= 1/6
(x) ottenere un numero pari come somma:
Sia E10 = evento di ottenere un numero pari come somma., Gli eventi di un numero pari come somma saranno E10 = = 18
Quindi, probabilità di ottenere ‘un numero pari come somma
Numero di risultati favorevoli
P(E10)= Numero totale di possibili risultati
= 18/36
= 1/2
(xi) ottenere un numero primo come somma:
Sia E11 = evento di ottenere un numero primo come somma., Gli eventi di un numero primo come la somma sarà E11 = = 15
Pertanto, la probabilità ofgetting ‘un numero primo come somma’
Numero di risultati favorevoli
P(E11) = numero Totale dei possibili risultati
= 15/36
= 5/12
(xii) ottenere adoublet anche di numeri:
Lasciate che E12 = evento di ottenere un doppietto di numeri pari., Gli eventi di una doppietta anche i numeri saranno E12 = = 3
Pertanto, la probabilità ofgetting ‘un doppietto di numeri pari’
Numero di risultati favorevoli
P(E12) = numero Totale dei possibili risultati
= 3/36
= 1/12
(xiii) per ottenere amultiple 2 su un dado e un multiplo di 3 su gli altri muoiono:
Lasciate che E13 = evento di ottenere un multiplo di 2, su un dado e un multiplo di 3 su gli altri muoiono., Gli eventi di un multiplo di 2 su un dado e un multiplo di 3 sull’altro dado saranno E13 = = 11
Quindi, probabilità di ottenere ‘un multiplo di 2 su un dado e un multiplo di 3 sull’altro dado ‘
Numero di risultati favorevoli
P (E13)= Numero totale di possibili risultati
= 11/36
4. Twodice sono lanciati. Trova (i) le probabilità a favore di ottenere la somma 5, e (ii) theodds contro ottenere la somma 6.
Soluzione:
Sappiamo che in un singolo lancio di due die, il numero totale di possibili risultati è (6 × 6) = 36.
Sia lo spazio campione. Quindi, n (S) = 36.,
(i) le probabilità a favore di ottenere la somma 5:
Sia E1 l’evento di ottenere la somma 5. Poi,
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒ P (E1) = 4
Pertanto, P(E1) = n (E1)/n (S) = 4/36 = 1/9
⇒ quote a favore di E1 = P(E1)/ = (1/9)/(1 – 1/9) = 1/8.
(ii) le probabilità di ottenere la somma 6:
Sia E2 l’evento di ottenere la somma 6. Quindi,
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒ P(E2) = 5
Quindi, P(E2) = n(E2)/n(S) = 5/36
⇒ probabilità contro E2 = /P(E2) = (1 – 5/36)/(5/36) = 31/5.
5., Due dadi, uno blu e uno arancione, vengono lanciati contemporaneamente. Trova la probabilità di ottenere
(i) numeri uguali su entrambi
(ii) due numeri che appaiono su di essi la cui somma è 9.,
Soluzione:
I risultati possibili sono:
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
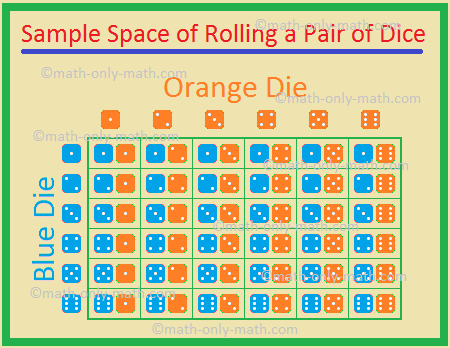
Pertanto, il numero totale di possibili esiti = 36.,
(i) Numero di risultati favorevoli per l’evento E
= numero di risultati con numeri uguali su entrambi i dadi
= 6 .
Così, per definizione, P(E) = \(\frac{6}{36}\)
= \(\frac{1}{6}\)
(ii) Numero di risultati favorevoli per l’evento F
= Numero di risultati in cui due numeri riportati su di essi sono la somma 9
= 4 .
Quindi, per definizione, P (F) = \(\frac{4}{36}\)
= \(\frac{1}{9}\).
Questi esempi aiuteranno a risolvere diversi tipi di problemi in base alla probabilità di lanciare due dadi.,p>Probability and Playing Cards
Probability for Rolling Two Dice
Solved Probability Problems
Probability for Rolling Three Dice
9th Grade Math
From Probability for Rolling Two Dice to HOME PAGE
















Lascia un commento