Vai alla Superficie o al volume.

Un prisma è un oggetto solido con:
- estremità identiche
- facce piane
- e la stessa sezione trasversale per tutta la sua lunghezza !
Una sezione trasversale è la forma fatta tagliando dritto attraverso un oggetto.
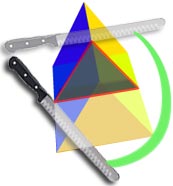
La sezione trasversale di questo oggetto è un triangolo …
.. ha la stessa sezione trasversale per tutta la sua lunghezza …
… quindi è un prisma triangolare.,
|
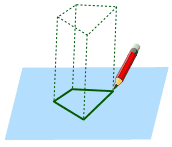
Prova a disegnare una forma su un pezzo di Quindi immagina che si estenda dal foglio di carta … |
 |
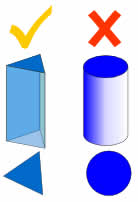
Senza Curve!
Un prisma è un poliedro, il che significa che tutte le facce sono piatte!
Nessun lato curvo.
Ad esempio, un cilindro non è un prisma, perché ha lati curvi.,
Basi
Le estremità di un prisma sono parallele
e ognuna è chiamata base.
Lati
Le facce laterali di un prisma sono parallelogrammi
(forme a 4 lati con lati opposti paralleli)
Questi sono tutti Prismi:
e altro ancora!

Esempio: Questo cristallo di ghiaccio esagonale.
Sembra un esagono, ma poiché ha un certo spessore è in realtà un prisma esagonale!
Fotografia della NASA / Alexey Kljatov.,
Prismi regolari vs irregolari
Tutti gli esempi precedenti sono Prismi regolari, perché la sezione trasversale è regolare (in altre parole è una forma con lunghezze di bordo uguali e angoli uguali.,)
Here is an example of an Irregular Prism:
| Irregular Pentagonal Prism: | ||
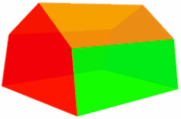 |
 |
|
| Cross-Section | ||
| It is “irregular” because the cross-section is not “regular” in shape.,div> Superficie = 2 × Area di Base
+ Perimetro di Base × Lunghezza Esempio: Qual è l’area della superficie di un prisma, in cui l’area di base è di 25 m2, il perimetro di base è di 24 m, e la lunghezza è di 12 m: Superficie = 2 × Area di Base + Perimetro di Base × Lunghezza
= 2 × 25 m2 + 24 m × 12 m
= 50 m2 + 288 m2
= 338 m2
(Nota: abbiamo una Zona Strumento di Calcolo) il Volume di un PrismaIl Volume di un prisma è l’area di una fine dei tempi, e la lunghezza del prisma., Volume = Area di Base × Lunghezza Esempio: Qual è il volume di un prisma, in cui l’area di base è di 25 m2 e 12 m di lunghezza: Volume = Area del × di Lunghezza
= 25 m2 × 12 m
= 300 m3
Giocare qui., La formula funziona anche quando si “sporge” (obliquo), ma ricordate che l’altezza è perpendicolare alla base: E questo è il motivo per cui:
© 2021 Tombouctou Tema di Anders Noren — Su ↑ | ||





















Lascia un commento