Oggi diamo un’occhiata alle opzioni più popolari modello di pricing. Il modello Black Scholes, noto anche come metodo Black-Scholes-Merton, è un modello matematico per i contratti di opzione dei prezzi. Funziona stimando la variazione degli strumenti finanziari. La tecnica si basa sul presupposto che i prezzi seguono una distribuzione lognormal. Sulla base di questo, deriva il valore di un’opzione.,

È più adatto per opzioni indipendenti dal percorso, che gli investitori non possono esercitare prima della data di scadenza. Ciò lo rende diverso dal modello binomiale di Pricing delle opzioni, che è un metodo neutrale al rischio per valutare le opzioni dipendenti dal percorso (ad esempio, opzioni americane).

Analisti e investitori considerano Black Scholes uno dei concetti essenziali nella moderna teoria finanziaria.

Introdotto nel 1973 nel Journal of Political Economy, da Fischer Black e Myron Scholes, e successivamente costruito su Robert Merton, il modello ha vinto il premio Nobel per l’economia nel 1997.,

Il modello segue un’equazione differenziale, che usiamo per risolvere i prezzi delle opzioni. Usiamo la variante standard del modello per le opzioni di stile europeo. Black Scholes non è adatto per le opzioni di stile americano, in quanto non considera gli investitori possono esercitare queste opzioni in qualsiasi momento prima della loro data di scadenza.

Il metodo presuppone che il prezzo del titolo sottostante segua una distribuzione lognormale, in quanto non può essere negativo. La distribuzione su cui si basa il modello si basa sul moto browniano, una teoria per predire i fenomeni casuali naturali.,

usiamo il modello di calcolare un preventivo per un’opzione di prezzo, utilizza le seguenti informazioni:

  • Il prezzo corrente;
  • Il prezzo di esercizio;
  • Tempo di scadenza;
  • dividendi Attesi;
  • Previsto tasso di interesse; e
  • volatilità attesa.

Inizialmente, il modello non considera l’effetto dei pagamenti dei dividendi. Pertanto è spesso adattato a farlo determinando il valore della data di stacco cedola dell’attività sottostante., Il dividend yield ha l’effetto di ridurre l’attuale prezzo delle azioni perché il titolare dell’opzione rinuncia ai dividendi.

Ipotesi

Il modello Black Scholes funziona solo se facciamo determinate ipotesi.,s verificarsi durante l’opzione durata di vita (questo è un presupposto del modello iniziale, che gli analisti hanno poiché risolto aggiungendo il rendimento del dividendo nel modello formula);

  • I mercati sono efficienti, significato siamo in grado di prevedere i loro movimenti;

  • Acquisto e la vendita di opzioni comportano nessun costo di transazione;
  • Sia la volatilità dell’attività sottostante, il tasso privo di rischio rimangano costanti fino alla data di scadenza, che non è corretta, in quanto in realtà la volatilità turni di domanda e offerta; e
  • I rendimenti del sottostante seguano una distribuzione normale.,

    • Formula di Black Scholes

    La formula del modello è abbastanza complessa matematicamente, il che non è un problema particolare, poiché possiamo impiegare strumenti specializzati per calcolarlo per noi. Ma è ancora essenziale capire come funziona.,

    Per calcolare il prezzo di un’opzione call, sotto Black Scholes, possiamo utilizzare la seguente equazione:

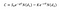
    in Cui:

    • S0 è il prezzo di riserva;
    • e è il numero esponenziale;
    • q è il dividend yield percentuale;
    • T è il termine (un anno sarà T=1, mentre sei mesi sarà T=0.,5);
    • N(d1) è il delta dell’opzione call, il che significa la variazione del prezzo di oltre il cambiamento del prezzo delle azioni;
    • K è il prezzo di esercizio;
    • r è il tasso privo di rischio; e
    • N(d2) è la probabilità che il futuro prezzo delle azioni sarà superiore al prezzo di esercizio, la probabilità che si eserciterà l’opzione.

    Un lato è il prezzo delle azioni moltiplicato per la distribuzione normale standard cumulativo di d1, e l’altro — il prezzo di esercizio, scontato al tempo T e poi moltiplicato per la distribuzione normale standard cumulativo di d2.,

    Dove siamo in grado di calcolare d1 e d2 con le seguenti formule:

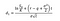
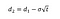
    Dove s è la volatilità dei rendimenti del sottostante.,

    Si può applicare la stessa logica per una opzione put:

    iscriviti alla nostra Newsletter per un LIBERO Excel Analisi di Benchmark Modello

    Esempio di Black Scholes Calcolo

    Per illustrare meglio il concetto che sta dietro il Black Scholes, diamo un’occhiata al il seguente modello. Iniziamo con gli input del modello., Come discusso sopra, abbiamo bisogno delle seguenti sei variabili per calcolare i valori delle opzioni call e put.

    a quel punto, calcoliamo le opzioni’ parametri. A partire da d1, otteniamo 0,39 dalle nostre ipotesi del modello.

    calcolare, abbiamo semplicemente trasferire la formula per il d1 di Excel.,

    Following the same approach, we calculate d2, N(d1) and N(d2).

    With those, we can calculate the Call Option Price and the Put Option Price.,

    E ‘ possibile utilizzare la Chiamata-Mettere principio di Parità di verificare se le nostre formule e calcoli sono corretti.

    Ora che abbiamo il nostro modello per calcolare le opzioni Call e Put i prezzi siamo in grado di fare un passo ulteriore e guardare come i diversi parametri di input influenzare i risultati del nostro modello., La funzionalità Tabella dati in Excel è un ottimo strumento per preparare alcune tabelle di analisi di sensibilità per le nostre variabili. Puoi imparare come utilizzare le tabelle di dati nel nostro articolo di analisi della sensibilità.

    Diamo un’occhiata al prezzo delle azioni se cambia da €10 a €100 e come influisce sulla chiamata e sui valori Put. Notiamo che l’opzione Call non ha alcun valore fino a quando il prezzo delle azioni non raggiunge €40. Vediamo il contrario per l’opzione Put, dove il suo valore raggiunge lo zero una volta che il prezzo delle azioni supera €85.,

    Se prepariamo la stessa tabella di sensibilità per il Prezzo, possiamo osservare la relazione inversa. All’aumentare del prezzo di esercizio, il valore di chiamata scende e il valore Put aumenta.

    diamo anche un’occhiata a rischio-free rate., Man mano che aumenta, questo aumenta anche il tasso di rendimento richiesto. Successivamente, questo diminuisce il valore delle scorte. Notiamo una relazione diretta, poiché il tasso privo di rischio aumenta, aumenta anche il valore dell’opzione Call, mentre il valore dell’opzione Put diminuisce il suo valore.

    di Seguito lo stesso approccio, si può andare avanti e guardare il resto dei parametri e come influenzano i Valori di Opzione., È possibile scaricare il modello di Excel alla fine di questo articolo e andare oltre l’analisi di sensibilità in là.

    È possibile scaricare il modello di esempio in Excel nell’articolo originale.

    Conclusione

    È importante ricordare che il modello Black-Scholes-Merton è un concetto teorico. Lo usiamo per cercare di stimare il comportamento del mercato. Tuttavia, quando usiamo i risultati nel nostro processo decisionale, dobbiamo capire le ipotesi sottostanti nel modello e come si discosta dalla realtà.,

    La formula ha aiutato il trading di opzioni a diventare più popolare, in quanto lo rende meno simile al gioco d’azzardo. Al giorno d’oggi, varie modifiche di Black Scholes sono ampiamente popolari come strategie fondamentali per il controllo del rischio, associate alla volatilità.

    Puoi mostrare il tuo sostegno condividendo l’articolo con colleghi e amici.