La media, la Mediana, la Modalità: Cosa Sono, Come trovarli

Suggerimenti per ricordare la differenza

Hai problemi a ricordare la differenza tra media, mediana e modalità? Ecco un paio di suggerimenti che possono aiutare. È inoltre possibile controllare i tutor a Chegg.com (i primi 30 minuti è gratis!).

• “A la mode” è una parola francese che significa alla moda ; Si riferisce anche a un modo popolare di servire il gelato. Quindi “Mode” è il membro più popolare o alla moda di un insieme di numeri. La modalità parola è anche come la maggior parte.,
• La” Media ” richiede di fare aritmetica (aggiungendo tutti i numeri e dividendo) in modo che sia quella “media”.
• “Mediana” ha lo stesso numero di lettere di “Medio”.

Non sono ancora sicuro di quale sia la differenza tra i tre? Guarda il video o continua a leggere per maggiori informazioni:

La media

Media vs. Mediana
Media vs., Media
“Mezzi” specifici comunemente usati nelle statistiche
Altri tipi

Media vs Mediana

Entrambi sono misure di dove si trova il centro di un set di dati (chiamato “Tendenza centrale” nelle statistiche), ma di solito sono numeri diversi. Ad esempio, prendi questo elenco di numeri: 10, 10, 20, 40, 70.

• La media (informalmente, la “media”) si trova sommando tutti i numeri insieme e dividendo per il numero di elementi nel set: 10 + 10 + 20 + 40 + 70 / 5 = 30.
• La mediana si trova ordinando l’insieme dal più basso al più alto e trovando il centro esatto., La mediana è solo il numero centrale: 20.

A volte i due saranno lo stesso numero. Ad esempio, il set di dati 1, 2, 4, 6, 7 ha una media di 1 + 2 + 4 + 6 + 7 / 5 = 4 e una mediana (un mezzo) di 4.

Media vs Media: qual è la differenza?

Quando hai iniziato in matematica, probabilmente ti è stato insegnato che una media era un importo “medio” per un insieme di numeri. Hai sommato i numeri, divisi per il numero di elementi che puoi e voilà! si ottiene la media. Ad esempio, la media di 10, 5 e 20 è:

10 + 6 + 20 = 36 / 3 = 12.,

Hai iniziato a studiare le statistiche e all’improvviso la “media” è ora chiamata media. Che cos’è successo? La risposta è che hanno lo stesso significato(sono sinonimi).

Detto questo, tecnicamente, la parola media è l’abbreviazione della media aritmetica. Usiamo parole diverse nelle statistiche, perché ci sono diversi tipi di mezzi, e tutti fanno cose diverse.

“Mezzi” specifici comunemente usati in Stats

Probabilmente ti imbatterai in questi nella tua classe stats., Hanno significati molto stretti:

• Media della distribuzione di campionamento: usata con le distribuzioni di probabilità, specialmente con il Teorema del Limite centrale. È una media di un insieme di distribuzioni.
• Media del campione: il valore medio in un campione.
• Popolazione media: il valore medio di una popolazione.

Kenney, J. F. e Keeping, E. S. Matematica delle statistiche, Pt. 1, 3a ed. Princeton, NJ: Van Nostrand, 1962.

Altri tipi

Esistono altri tipi di mezzi e li utilizzerai in vari rami della matematica., La maggior parte ha applicazioni molto ristrette a campi come la finanza o la fisica; se sei in statistiche elementari probabilmente non lavorerai con loro.

Questi sono alcuni dei tipi più comuni che incontrerai.

1. Media ponderata.
2. Media armonica.
3. Media geometrica.
4. Media aritmetica-geometrica.
5. Radice-Media Media quadrata.
6. Media heroniana.
7. Media grafica

1. Media ponderata

   Questi sono abbastanza comuni nelle statistiche, specialmente quando si studiano le popolazioni., Invece di ogni punto dati che contribuisce in modo uguale alla media finale, alcuni punti dati contribuiscono più di altri. Se tutti i pesi sono uguali, allora questo sarà uguale alla media aritmetica. Ci sono alcune circostanze in cui questo può dare informazioni errate, come mostrato dal Paradosso di Simpson.

2. Media armonica

   

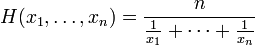
   La formula armonica.

   Per trovarlo:

   1. Aggiungi i reciproci dei numeri nel set., Per trovare un reciproco, capovolgere la frazione in modo che il numeratore diventi il denominatore e il denominatore diventi il numeratore. Ad esempio, il reciproco di 6/1 è 1/6.
   2. Dividi la risposta per il numero di elementi nel set.
   3. Prendi il reciproco del risultato.

   La media armonica è usata molto in fisica. In alcuni casi che coinvolgono tassi e rapporti dà una media migliore rispetto alla media aritmetica. Troverete anche usi in geometria, finanza e informatica.,

3. Media geometrica

   
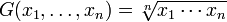
   Questo tipo ha usi molto ristretti e specifici in finanza, scienze sociali e tecnologia. Ad esempio, diciamo che possiedi titoli che guadagnano il 5% il primo anno, il 20% il secondo anno e il 10% il terzo anno. Se si desidera conoscere il tasso medio di rendimento, non è possibile utilizzare la media aritmetica. Perché? Perché quando stai trovando tassi di rendimento stai moltiplicando, non aggiungendo. Ad esempio, il primo anno si sta moltiplicando per 1,05.,

4. Media aritmetica-geometrica

   Questo è usato principalmente nel calcolo e nel calcolo della macchina (cioè come base per molti calcoli al computer). E ‘ legato al perimetro di un’ellisse. Quando fu sviluppato per la prima volta da Gauss, fu usato per calcolare le orbite planetarie. L’aritmetica-geometrica è (non sorprendentemente!) una miscela delle medie aritmetiche e geometriche. La matematica è piuttosto complicata, ma puoi trovare una spiegazione relativamente semplice della matematica qui.,

5. Root-Mean Square

   È molto utile nei campi che studiano le onde sinusoidali, come l’ingegneria elettrica. Questo particolare tipo è anche chiamato la media quadratica. Vedi: Quadratica Media / Radice Media quadrata.

6. Media heroniana

   Utilizzata in geometria per trovare il volume di un tronco piramidale. Un tronco piramidale è fondamentalmente una piramide con la punta tagliata.

7. Media grafica

   Un altro nome per la pendenza della linea secante: l’equivalente del tasso medio di variazione tra due punti.,
   

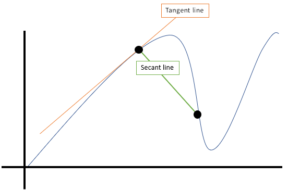
Qual è la modalità?

La modalità è il numero più comune in un set. Ad esempio, la modalità in questo insieme di numeri è 21:
21, 21, 21, 23, 24, 26, 26, 28, 29, 30, 31, 33

Qual è la mediana?

La mediana è il numero centrale in un set di dati. Per trovare la mediana, elencare i punti dati in ordine crescente e quindi trovare il numero centrale., Il numero al centro di questo set 28, come ci sono 4 numeri al di sotto di esso e 4 numeri di cui sopra:
23, 24, 26, 26, 28, 29, 30, 31, 33

Come trovare la media, la mediana e la modalità di mano: Passi

Come trovare la media, la mediana e modalità: MODALITÀ:

Come trovare la media, la mediana e modalità: MEDIA

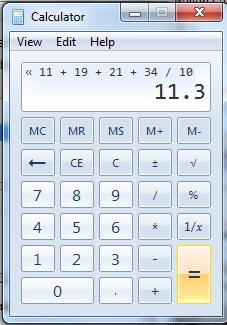
Dividere la somma per il numero di elementi per trovare la media.

Come trovare la media, la mediana e la modalità: MEDIANA

Se hai un numero dispari nel passaggio 3, vai al passaggio 5. Se hai un numero pari, vai al passaggio 6.,

Suggerimento: puoi avere più di una modalità. Ad esempio, la modalità di 1, 1, 5, 5, 6, 6 è 1, 5 e 6.

Come la spiegazione? Dai un’occhiata al Practically Cheating Statistics Handbook, che ha centinaia di più soluzioni passo-passo, proprio come questo!

SPSS Mean mode mediana

Per trovare la SPSS mean mode mediana, è necessario utilizzare la scheda Frequenza. Sembra un po ‘ contro-intuitivo, ma la scheda Statistiche descrittive non ti dà la possibilità di trovare la modalità o la mediana.,

SPSS ha un’interfaccia molto simile a Microsoft Excel. Pertanto, se hai già utilizzato Microsoft Excel, ti adatterai rapidamente a SPSS.

SPSS Mean Mode Mediana: Passi

Guarda il video o leggi i passaggi seguenti:

Domanda di esempio: Trova la mediana della modalità media SPSS per il seguente set di dati: 20,23,35,66,55,66

Passaggio 1: Apri SPSS. Nel “Cosa ti piacerebbe fare?”finestra di dialogo, fare clic sul pulsante di opzione” digita dati” e quindi fare clic su ” OK.”Si aprirà un nuovo foglio di lavoro., Nota: se hai disattivato la prima schermata di aiuto, questa opzione potrebbe non essere visualizzata. In tal caso, basta iniziare al punto 2.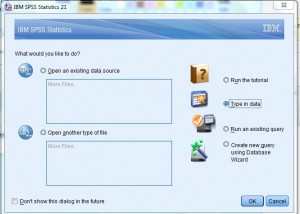

Passo 2: Digitare i dati nel foglio di lavoro. È possibile digitare i dati in una colonna o più colonne se si dispone di più set di dati. Per questo esempio, digitare 20, 23, 35, 66, 55, 66 nella colonna 1. Non lasciare spazi tra i dati (cioè non lasciare righe vuote).

Passo 2: Fai clic su “Analizza”, passa il mouse su “Statistiche descrittive” e quindi fai clic su ” Frequenze.,”

Passo 3: Fare clic su “Statistiche” e quindi selezionare le caselle ” media”, “modalità” e ” mediana.”Fai clic su” Continua” due volte (seleziona “nessuno” come tipo di grafico nella seconda finestra).
Nota: in alcune versioni di SPSS, potrebbe essere necessario fare clic su “Continua” una sola volta e potrebbe non fornire un’opzione per il tipo di grafico.

I risultati della frequenza appariranno come output. La parte superiore dell’output visualizzerà la media, la modalità e la mediana.

Se scorri verso il basso, la tabella delle frequenze ti mostrerà anche la modalità., La modalità è definita nelle statistiche come il numero con la frequenza più alta (per questo set di dati campione, il numero che appare di più è 66, con due risultati nella colonna frequenza).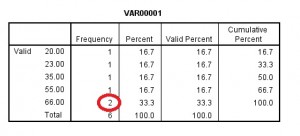

TI 83 Media, Mediana e Modalità

Trovare la media TI 83 o la mediana TI 83 da un elenco di dati può essere ottenuto in due modi: inserendo un elenco di dati o utilizzando la schermata iniziale per digitare i comandi., Utilizzando la funzione elenco è altrettanto facile come inserire i dati nella schermata iniziale, e ha il vantaggio aggiunto che è possibile utilizzare i dati per altri scopi dopo aver calcolato la media, la modalità e la mediana (ad esempio, si potrebbe desiderare di creare un istogramma TI 83).

Passi per la Media, la mediana e la modalità sul TI 83

Guarda il video per la media e la mediana o leggi i passaggi sottostanti (per la modalità, vedi questa nota):

Passo 1: Inserire i dati di cui sopra in un elenco., Premere il pulsante STAT e quindi premere INVIO. Immettere il primo numero (1250), quindi premere INVIO. Continuare a inserire i numeri, premendo il pulsante INVIO dopo ogni voce.

Passo 2: Premere il pulsante STAT.

Passo 3: Premere il pulsante freccia destra per evidenziare ” Calc.”

Passo 4: Premere INVIO per scegliere “1-Var Stats” e quindi digitare il nome della lista. Ad esempio, per inserire L1 premere e .

Passo 5: Premere nuovamente INVIO. La calcolatrice restituirà la media, x. Per questo elenco di dati, la media TI 83 è di 884,05 piedi (arrotondato a 3 cifre decimali).

Passo 6: Freccia verso il basso fino a vedere ” Med.,”Questo è il TI 83 mediana; per i dati di cui sopra, la mediana è 813.05 piedi.

Nota: Il TI-83 plus non ha una funzione di modalità integrata, ma una volta inserito l’elenco, è abbastanza facile individuare la modalità: è solo il numero che si verifica più spesso nel set. Non sei sicuro? Per saperne di più sulla modalità qui.

Questo è tutto!

Hai perso la tua guida? Scarica uno nuovo qui al sito TI.

——————————————————————————

Hai bisogno di aiuto con un compito a casa o una domanda di prova?, Con Chegg Studio, è possibile ottenere soluzioni passo-passo alle vostre domande da un esperto del settore. I tuoi primi 30 minuti con un tutor Chegg sono gratuiti!