Uomini. Sento, in qualche modo, che mi piace quello che stai dicendo.
Soc. E io, Meno, mi piace quello che sto dicendo.
dal Meno di Platone
La lunghezza della diagonale del quadrato unitario è uguale alla radice quadrata di 2.
La lunghezza della diagonale del quadrato unitario è uguale a √2. Beh, questa non e ‘ una gran notizia. Chiunque abbia mai incontrato il teorema di Pitagora è consapevole del fatto., Nel triangolo rettangolo isoscele con le gambe di lunghezza 1, l’ipotenusa, secondo il teorema di Pitagora – 12 + 12 = (ipotenusa) 2 – è infatti di lunghezza √2. La motivazione di questa pagina non è tanto quel fatto in sé, ma il modo di mostrarlo senza ricorrere al famoso teorema. In effetti, si potrebbe sostenere che il teorema di Pitagora potrebbe essere stato abusato, vedi un curioso esempio.
Un argomento che risale alla figura disegnata da Socrate nel Meno di Platone potrebbe essere stato conosciuto da Pitagora stesso, anche se quest’ultimo ha vissuto un secolo prima.,
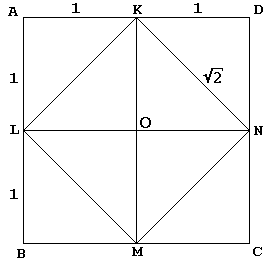
Nella finestra di dialogo, Socrate, nel suo solito modo, conduce un giovane schiavo a una costruzione di un quadrato due volte l’area di quello dato:
Il quadrato dato KLMN con centro O viene prima tagliato dalle sue diagonali in 4 triangoli uguali. Socrate incorpora KLMN in un ABCD quadrato più grande come se riflettesse questi triangoli ciascuno nella sua ipotenusa. Lo schiavo allora ammette – e chi non lo farebbe? – quell’ABCD quadrato è due volte più grande del KLMN quadrato.
A dire il vero, il quadrato ABCD di Socrate misurava 4 sul lato, in modo tale che il quadrato KLMN avesse un’area di 8., È chiaro che quando iniziamo con il quadrato ABCD del lato 2 (e quindi dell’area 4), il quadrato KLMN avrà un’area di 2.
Ora, in generale, per un numero positivo A, √A è definito come un numero il cui quadrato è A:
(√A)2.
D’altra parte, ogni studente di aree sa, che l’area di un quadrato di lato b è uguale a b2. Ne consegue che il lato di un quadrato con area A è esattamente √A. Concludiamo che il lato del quadrato KLMN è uguale a √2. Per uno,
KN = √A.
Il punto centrale dell’argomento è il fatto che, nel diagramma, KN svolge un doppio ruolo., Oltre ad essere uno dei lati del quadrato KLMN, serve anche come diagonale di quadrato OKDN. Quest’ultimo è ovviamente un quadrato unitario, che dimostra la nostra affermazione.
(Da una prospettiva leggermente diversa lo stesso episodio è menzionato altrove.)
















Lascia un commento