Un numero pari è un numero intero che può essere diviso esattamente o uniformemente per \color{red}2. Se un numero è esattamente diviso per \ color {red}2, ciò implica che il numero in questione ha un resto di \color{blue}0 sulla divisione di \color{red}2.
Eseguendo la matematica mentale, è ovvio che i numeri sottostanti, inclusi i numeri negativi, sono pari perché sono tutti divisibili per 2.,

Inoltre, voglio sottolineare che molti studenti pensano che zero non sia né pari né dispari.
Credimi, zero è considerato come un numero pari per la stessa semplice ragione che è anche un numero intero divisibile per 2, quindi nessun resto quando diviso per 2. Cioè, 0 \ div 2 = 0.
Osservazione: Dagli esempi sopra, possiamo facilmente generalizzare che i numeri pari terminano sempre con una cifra di 0, 2, 4, 6 o 8.,
Tuttavia, esiste un modo migliore per definire un numero pari perché è più matematicamente preciso. Eccola!
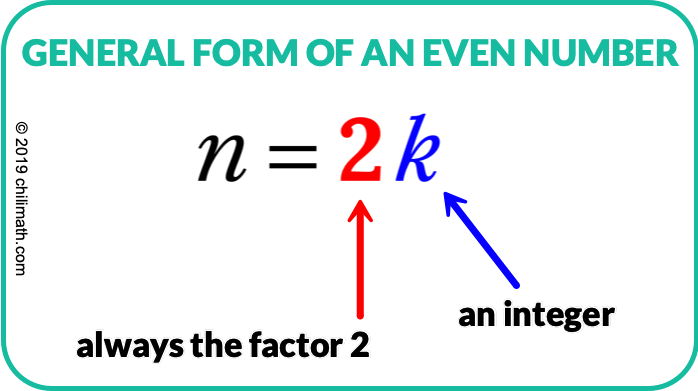
Forma Generale di un Numero
Esempi di Numeri Espressi in Forma Generale
Mettiamo la forma generale di un numero pari alla prova. Qualunque sia il concetto di matematica che ci viene presentato, è fondamentale verificarlo. Dovrebbe in qualche modo avere senso per noi prima di includerlo nella nostra “casella degli strumenti matematici”.,
Di seguito sono riportati alcuni esempi per mostrare il concetto di un numero pari come n = 2\,k dove k è un numero intero.
\color{red}\LARGE {n = 2k}
- 0 \0 = 2\left( 0 \right)
- 14 \14 = 2\left( 7 \right)
- – 32 \a – 32 = 2\left( { – 16} \right)
- 50 \50 = 2\left( {25} \right)
- – 78 \a – 78 = 2\left( { – 39} \right)
La comparsa costante di 2 come uno dei fattori di un numero pari, suggerisce che anche i numeri, in effetti, sono un multiplo di 2.,
Potresti anche essere interessato a:
Che cos’è un numero dispari?
Elenco di numeri pari
Elenco di numeri dispari
















Lascia un commento