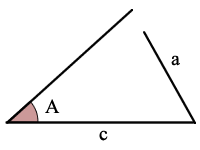
Triangolo Figura Angolo-Lato-Angolo (ASA)
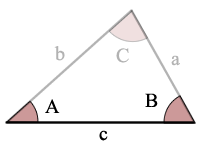
A = angolo di Un
B = angolo B
C = angolo C
a = lato
b = lato b
c = lato c
P = perimetro
s = semi-perimetrale
K = area
r = raggio del cerchio inscritto
R = raggio del cerchio circoscritto
Calcolatrice Uso
Ogni opzione di calcolo, riportato di seguito, è sub-proiettili che elencare la sequenza dei metodi utilizzati in questo calcolatore per risolvere unknown angolo e lato di valore, tra cui la Somma degli Angoli in un Triangolo, teorema dei seni e la Legge del Coseno., Queste NON sono le UNICHE sequenze che potresti usare per risolvere questi tipi di problemi.
- Consultare anche questi Trigonometria Calcolatori:
- la Legge del Coseno Calcolatrice
- Legge di Sines Calcolatrice
Risolvere un Triangolo Teoremi
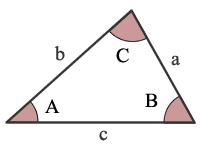
AAA angolo, Angolo, Angolo
Specificare i tre angoli di un triangolo non identificare in modo univoco un triangolo. Pertanto, specificare due angoli di un tringle consente di calcolare solo il terzo angolo.,
Date le dimensioni di 2 angoli di un triangolo è possibile calcolare la dimensione del terzo angolo. Il totale sarà uguale a 180 ° o π radianti.
C = 180° – A – B (in gradi)
C = π – A – B (in radianti)
AAS è Angolo, Angolo, Lato
Data la dimensione di 2 angoli e 1 lato opposto a uno degli angoli dati, è possibile calcolare le dimensioni del restante 1 angolo e 2 lati.
usa la regola della Somma degli angoli per trovare l’altro angolo, quindi
usa la Legge dei Seni per risolvere per ciascuno degli altri due lati.,
ASA è Angolo, Lato, Angolo
Data la dimensione di 2 angoli e la dimensione del lato che si trova tra questi 2 angoli è possibile calcolare le dimensioni del restante 1 angolo e 2 lati.
usa la regola della Somma degli angoli per trovare l’altro angolo, quindi
usa la Legge dei Seni per risolvere per ciascuno degli altri due lati.,
ASS (o SSA) è Angle, Side, Side
Data la dimensione di 2 lati (a e c dove a< c) e la dimensione dell’angolo A che non è tra questi 2 lati potresti essere in grado di calcolare le dimensioni del restante 1 lato e 2 angoli, a seconda delle seguenti condizioni.,f Semplici da risolvere per ciascuno degli altri due angoli
presenti 2 soluzioni
Esempio: 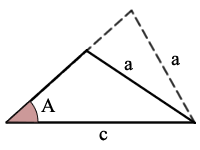
sin(A) = a/c, c’è un possibile triangolo
utilizzare Il teorema dei seni per risolvere in un angolo, C
utilizzare la Somma di Angoli Regola per trovare l’altro angolo, B
utilizzare Il teorema dei seni per risolvere l’ultimo lato, b
Esempio: 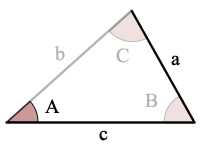
sin(A) > a/c, non c’è possibilità di triangoli
Avviso di Errore: sin(A) > a/c, quindi non ci sono soluzioni e non a triangolo!,
Esempio:
SAS è Side, Angle, Side
Data la dimensione di 2 lati (c e a) e la dimensione dell’angolo B che si trova tra questi 2 lati è possibile calcolare le dimensioni dei restanti 1 lato e 2 angoli.
usa la Legge dei coseni per risolvere il lato rimanente, b
determina quale lato, a o c, è più piccolo e usa la Legge dei Seni per risolvere la dimensione dell’angolo opposto, A o C rispettivamente.,
usa la regola della Somma degli angoli per trovare l’ultimo angolo
SSS è Side, Side, Side
Date le dimensioni dei 3 lati puoi calcolare le dimensioni di tutti e 3 gli angoli nel triangolo.
usa la Legge dei coseni per risolvere gli angoli. Potresti anche usare la regola della Somma degli angoli per trovare l’angolo finale una volta che ne conosci 2.,peccato-1
la Legge del Coseno
Se a, b e c sono le lunghezze dei lati di un triangolo, di fronte agli angoli A, B e C, rispettivamente); poi la legge del coseno afferma:
a2 = c2 + b2 – 2bc cos A, la risoluzione per cos A, cos A = ( b2 + c2 – a2 ) / 2bc
b2 = a2 + c2 – 2ca cos B, la risoluzione per cos B cos B = ( c2 + a2 – b2 ) / 2ca
c2 = b2 + a2 – 2ab cos C, la risoluzione per cos C cos C = ( a2 + b2 – c2 ) / 2ab
Risolvere, per esempio, per un angolo, A = cos-1
Altri Triangolo Caratteristiche
Triangolo di perimetro P = a + b + c
Triangolo semi-perimetrale, s = 0.,5 * (a + b + c)
Area del triangolo, K = √
Raggio del cerchio inscritto nel triangolo, r = √
Raggio del cerchio circoscritto attorno al triangolo, R = (abc) / (4K)
Riferimenti/ Ulteriori letture
Weisstein, Eric W. “Teorema ASS.”Da MathWorld A una risorsa Web Wolfram. Teorema del CULO.
La matematica è divertente-Risolvere triangoli SAS
















Lascia un commento