Mostra avviso mobile Mostra tutte le note Nascondi tutte le note
Sezione 3-1 : Equazioni Parametriche e Curve
A questo punto (in entrambi i analisi matematica I e analisi matematica II) abbiamo guardato quasi esclusivamente a funzioni nella forma \(y = f\left( x \right)\) o \(x = h\left( y \right)\) e quasi tutte le formule che abbiamo sviluppato richiedono che le funzioni di essere in una di queste due forme. Il problema è che non tutte le curve o equazioni che vorremmo guardare cadono facilmente in questa forma.
Prendi, ad esempio, un cerchio. È abbastanza facile scrivere l’equazione di un cerchio centrato all’origine con radius \(r\).,
\
Tuttavia, non saremo mai in grado di scrivere l’equazione di un cerchio verso il basso come una singola equazione in una delle forme sopra. Certo possiamo risolvere per \(x\) o \(y\) come le seguenti due formule mostrano
\
ma ci sono in realtà due funzioni in ognuna di queste. Ogni formula dà una porzione del cerchio.
\
Sfortunatamente, di solito stiamo lavorando sull’intero cerchio, o semplicemente non possiamo dire che lavoreremo solo su una parte di esso. Anche se possiamo restringere le cose a una sola di queste parti, la funzione è ancora spesso abbastanza spiacevole da lavorare.,
\
Questa terza variabile è solitamente indicata da \(t\) (come abbiamo fatto qui) ma non deve essere ovviamente. A volte limiteremo i valori di \(t\) che useremo e altre volte no. Questo spesso dipenderà dal problema e da ciò che stiamo tentando di fare.
Per aiutare a visualizzare solo ciò che una curva parametrica è finta che abbiamo un grande serbatoio di acqua che è in costante movimento e facciamo cadere una pallina da ping pong nel serbatoio., Il punto \(\left( {x,y} \right) = \left( {f\left( t \right),g\left( t \right)} \right)\), quindi, rappresentano la posizione della pallina da ping-pong nel serbatoio al momento \(t\) e la curva parametrica sarà una traccia di tutte le sedi della pallina da ping-pong. Si noti che questa non è sempre un’analogia corretta, ma è utile inizialmente per aiutare a visualizzare solo cos’è una curva parametrica.
Disegnare una curva parametrica non è sempre una cosa facile da fare. Diamo un’occhiata a un esempio per vedere un modo di disegnare una curva parametrica., Questo esempio illustrerà anche perché questo metodo di solito non è il migliore.
A questo punto la nostra unica opzione per disegnare una curva parametrica è scegliere i valori di \(t\), inserirli nelle equazioni parametriche e quindi tracciare i punti. Quindi, inseriamo alcuni \(t\).,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Sfortunatamente, non c’è una vera risposta a questa domanda a questo punto. Scegliamo semplicemente \(t\) finché non siamo abbastanza sicuri di avere una buona idea di come appare la curva. È questo problema con la scelta di valori “buoni” di \(t\) che rende questo metodo di disegnare curve parametriche una delle scelte più povere. A volte non abbiamo scelta, ma se abbiamo una scelta dovremmo evitarla.
Discuteremo un metodo grafico alternativo negli esempi successivi che aiuterà a spiegare come sono stati scelti questi valori di \(t\).,
Abbiamo un’altra idea da discutere prima di disegnare effettivamente la curva. Le curve parametriche hanno una direzione di movimento. La direzione del movimento è data aumentando \(t\). Quindi, quando si tracciano curve parametriche, includiamo anche frecce che mostrano la direzione del movimento. Spesso daremo il valore di \(t\) che ha dato anche punti specifici sul grafico per chiarire il valore di\ (t\) che ha dato quel particolare punto.
Ecco lo schizzo di questa curva parametrica.
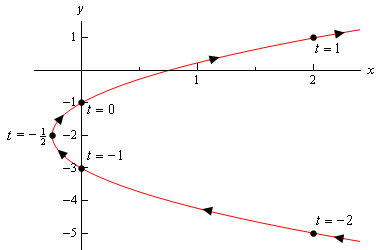
Quindi, sembra che abbiamo una parabola che si apre a destra.,
Prima di terminare questo esempio c’è un punto un po ‘ importante e sottile che dobbiamo discutere prima. Si noti che abbiamo fatto in modo di includere una parte dello schizzo a destra dei punti corrispondenti a \(t = – 2\) e \(t = 1\) per indicare che ci sono porzioni dello schizzo lì. Se avessimo semplicemente fermato lo schizzo in quei punti, stiamo indicando che non c’era alcuna porzione della curva a destra di quei punti e chiaramente ci sarà. Non abbiamo calcolato nessuno di questi punti.,
Questo può sembrare un punto non importante, ma come vedremo nel prossimo esempio è più importante di quanto potremmo pensare.
Prima di affrontare un modo molto più semplice per disegnare questo grafico affrontiamo prima il problema dei limiti sul parametro. Nell’esempio precedente non avevamo limiti sul parametro. Senza limiti sul parametro il grafico continuerà in entrambe le direzioni come mostrato nello schizzo sopra.
Avremo spesso dei limiti sul parametro tuttavia e questo influenzerà lo schizzo delle equazioni parametriche., Per vedere questo effetto diamo un’occhiata a una leggera variazione dell’esempio precedente.
Si noti che l’unica differenza qui è la presenza dei limiti su\(t\). Tutti questi limiti ci dicono che non possiamo prendere alcun valore di \(t\) al di fuori di questo intervallo. Pertanto, la curva parametrica sarà solo una parte della curva sopra. Ecco la curva parametrica per questo esempio.,
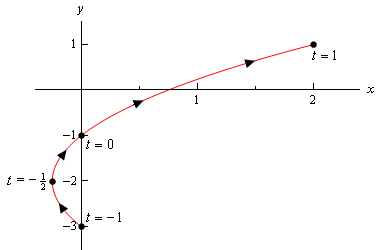
Si noti che con questo schizzo abbiamo iniziato e fermato lo schizzo proprio sui punti originati dai punti finali dell’intervallo di \(t\). Contrasto con lo schizzo nell’esempio precedente in cui avevamo una porzione dello schizzo a destra dei punti “start” e “end” che abbiamo calcolato.
In questo caso la curva inizia da \(t = – 1\) e termina da \(t = 1\), mentre nell’esempio precedente la curva non iniziava realmente nei punti più giusti che abbiamo calcolato., Dobbiamo essere chiari nei nostri schizzi se la curva inizia/finisce proprio in un punto, o se quel punto era semplicemente il primo/ultimo che abbiamo calcolato.
È giunto il momento di dare un’occhiata a un metodo più semplice per disegnare questa curva parametrica. Questo metodo utilizza il fatto che in molti casi, ma non in tutti, possiamo effettivamente eliminare il parametro dalle equazioni parametriche e ottenere una funzione che coinvolge solo \(x\) e \(y\). A volte chiameremo questa equazione algebrica per differenziarla dalle equazioni parametriche originali., Ci saranno due piccoli problemi con questo metodo, ma sarà facile affrontare questi problemi. È importante notare tuttavia che non saremo sempre in grado di farlo.
Il modo in cui eliminiamo il parametro dipenderà dalle equazioni parametriche che abbiamo. Vediamo come eliminare il parametro per l’insieme di equazioni parametriche con cui abbiamo lavorato fino a questo punto.
Ottenere uno schizzo della curva parametrica una volta eliminato il parametro sembra abbastanza semplice. Tutto quello che dobbiamo fare è tracciare l’equazione che abbiamo trovato eliminando il parametro., Come già notato, tuttavia, ci sono due piccoli problemi con questo metodo. Il primo è la direzione del movimento. L’equazione che coinvolge solo \(x\) e \(y\) NON darà la direzione del movimento della curva parametrica. Questo è generalmente un problema facile da risolvere tuttavia. Diamo una rapida occhiata alle derivate delle equazioni parametriche dall’ultimo esempio. Sono,
\
Si noti che la derivata \(x\) non è così utile per questa analisi in quanto sarà sia positiva che negativa e quindi \(x\) sarà sia crescente che decrescente a seconda del valore di \(t\)., Ciò non aiuta con la direzione, poiché seguire la curva in entrambe le direzioni mostrerà sia l’aumento che la diminuzione \(x\).
In alcuni casi, solo una delle equazioni, come questo esempio, darà la direzione mentre in altri casi potrebbe essere utilizzata una delle due. È anche possibile che, in alcuni casi, entrambi i derivati sarebbero necessari per determinare la direzione. Sarà sempre dipendente dal singolo insieme di equazioni parametriche.,
Il secondo problema con l’eliminazione del parametro è meglio illustrato in un esempio poiché ci troveremo in questo problema negli esempi rimanenti.
Ok, questo è stato un esempio molto lungo. La maggior parte di questi tipi di problemi non sono così a lungo. Abbiamo appena avuto un sacco di discutere in questo modo abbiamo potuto ottenere un paio di idee importanti fuori strada. Il resto degli esempi in questa sezione non dovrebbe richiedere tanto tempo per passare.
Ora, diamo un’occhiata a un altro esempio che illustrerà un’idea importante sulle equazioni parametriche.,
Quindi, abbiamo visto negli ultimi due esempi due serie di equazioni parametriche che in qualche modo hanno dato lo stesso grafico. Tuttavia, poiché hanno tracciato il grafico un numero diverso di volte, abbiamo davvero bisogno di considerarli come curve parametriche diverse almeno in qualche modo. Questa può sembrare una differenza di cui non dobbiamo preoccuparci, ma come vedremo nelle sezioni successive questa può essere una differenza molto importante. In alcune delle sezioni successive avremo bisogno di una curva che viene tracciata esattamente una volta.,
Prima di passare ad altri problemi, riconosciamo brevemente cosa succede cambiando il \(t\) in un nt in questo tipo di equazioni parametriche. Quando abbiamo a che fare con equazioni parametriche che coinvolgono solo seni e coseni ed entrambi hanno lo stesso argomento se cambiamo l’argomento da \(t\) a nt, cambiamo semplicemente la velocità con cui viene tracciata la curva. Se \(n > 1\) aumenteremo la velocità e se \(n < 1\) diminuiremo la velocità.
Diamo un’occhiata ad un paio di altri esempi.,
A questo punto abbiamo visto esempi che traccerebbero il grafico completo che abbiamo ottenuto eliminando il parametro se abbiamo preso un intervallo abbastanza ampio di \(t\). Tuttavia, nell’esempio precedente abbiamo visto che questo non sarà sempre il caso. È più che possibile avere un insieme di equazioni parametriche che tracciano continuamente solo una parte della curva. Di solito possiamo determinare se ciò accadrà cercando i limiti su \(x\) e \(y\) che ci sono imposti dall’equazione parametrica.,
Useremo spesso equazioni parametriche per descrivere il percorso di un oggetto o di una particella. Diamo un’occhiata a un esempio di questo.
Dovremmo dare un piccolo avvertimento a questo punto. A causa delle idee coinvolte in esse ci siamo concentrati su curve parametriche che ripercorrevano porzioni della curva più di una volta. Non, tuttavia, ottenere troppo bloccato nell’idea che questo accadrà sempre. Molte, se non la maggior parte delle curve parametriche tracceranno solo una volta. Il primo che abbiamo esaminato è un buon esempio di questo. Quella curva parametrica non ripeterà mai alcuna porzione di se stessa.,
C’è un ultimo argomento da discutere in questa sezione prima di andare avanti. Finora abbiamo iniziato con equazioni parametriche ed eliminato il parametro per determinare la curva parametrica.
Tuttavia, ci sono momenti in cui vogliamo andare dall’altra parte. Data una funzione o un’equazione potremmo voler scrivere un insieme di equazioni parametriche per esso. In questi casi diciamo che parametrizziamo la funzione.
Se prendiamo gli esempi 4 e 5 come esempi possiamo farlo per ellissi (e quindi cerchi)., Data l’ellisse
\
un insieme di equazioni parametriche per esso sarebbe,
\
Questo insieme di equazioni parametriche traccerà l’ellisse a partire dal punto \(\left( {a,0} \right)\) e traccerà in senso antiorario e traccerà esattamente una volta nell’intervallo \(0 \le t \le 2\pi \). Questo è un insieme abbastanza importante di equazioni parametriche come usato continuamente in alcuni soggetti con trattare con ellissi e / o cerchi.
Ogni curva può essere parametrizzata in più di un modo. Uno dei seguenti parametri parametrizzerà anche la stessa ellisse.,
\
La presenza di \(\omega \) cambierà la velocità che l’ellisse ruota come abbiamo visto nell’esempio 5. Si noti inoltre che gli ultimi due tracceranno ellissi con una direzione di movimento in senso orario (si potrebbe voler verificare questo). Si noti inoltre che non inizieranno tutti nello stesso punto (se pensiamo a \(t = 0\) come punto di partenza).
Ci sono molte altre parametrizzazioni di un’ellisse, naturalmente, ma si ottiene l’idea. È importante ricordare che ogni parametrizzazione traccerà la curva una volta con un intervallo potenzialmente diverso di \ (t\)., Ogni parametrizzazione può ruotare con diverse direzioni di movimento e può iniziare in punti diversi.
Potresti scoprire che hai bisogno di una parametrizzazione di un’ellisse che inizia in un determinato luogo e ha una particolare direzione di movimento e quindi ora sai che con un po ‘ di lavoro puoi scrivere una serie di equazioni parametriche che ti daranno il comportamento che stai cercando.
Ora, scriviamo un paio di altre importanti parametrizzazioni e tutti i commenti sulla direzione del movimento, il punto di partenza e l’intervallo di \(t\) per una traccia (se applicabile) sono ancora veri.,
Innanzitutto, poiché un cerchio non è altro che un caso speciale di un’ellisse, possiamo usare la parametrizzazione di un’ellisse per ottenere anche le equazioni parametriche per un cerchio centrato all’origine del raggio \(r\). Un modo possibile per parametrizzare un cerchio è,
\ \
A questo punto potrebbe non sembrare così utile fare una parametrizzazione di una funzione come questa, ma ci sono molti casi in cui sarà effettivamente più facile, o potrebbe anche essere richiesto, lavorare con la parametrizzazione invece della funzione stessa., Sfortunatamente, quasi tutte queste istanze si verificano in un corso di calcolo III.
















Lascia un commento