Mostra avviso mobile Mostra tutte le note Nascondi tutte le note
Sezione 4-11 : Approssimazioni lineari
In questa sezione daremo un’occhiata a un’applicazione non di derivate ma della linea tangente a una funzione. Naturalmente, per ottenere la linea tangente abbiamo bisogno di prendere derivati, quindi in qualche modo questa è anche un’applicazione di derivati.
\
Dai un’occhiata al seguente grafico di una funzione e della sua linea tangente.
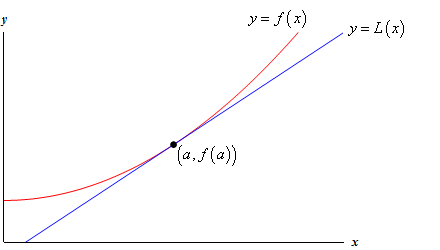
Quindi, perché dovremmo farlo? Diamo un’occhiata a un esempio.,
Le approssimazioni lineari fanno un ottimo lavoro di approssimazione dei valori di \(f\left( x \right)\) finché rimaniamo “vicino” \(x = a\). Tuttavia, più lontano da \(x = a\) otteniamo il peggio l’approssimazione è suscettibile di essere. Il problema principale qui è che quanto vicino dobbiamo rimanere su \(x = a\) per ottenere una buona approssimazione dipenderà sia dalla funzione che stiamo usando sia dal valore di \(x = a\) che stiamo usando. Inoltre, spesso non ci sarà un modo semplice per prevedere quanto lontano da \(x = a\) possiamo ottenere e avere ancora una “buona” approssimazione.,
Diamo un’occhiata a un altro esempio che in realtà è usato abbastanza pesantemente in alcuni punti.
Questa è in realtà un’approssimazione lineare un po ‘ importante. In ottica questa approssimazione lineare viene spesso utilizzata per semplificare le formule. Questa approssimazione lineare è anche usato per aiutare a descrivere il movimento di un pendolo e vibrazioni in una stringa.
















Lascia un commento