I vettori sono ampiamente utili nella scienza per descrivere qualsiasi cosa che abbia sia una direzione che una magnitudine. Di solito sono disegnati con l’aiuto di frecce appuntite, la cui lunghezza rappresenterà la grandezza del vettore. Il passaggio di un quarterback è l’esempio semplice perché ha la direzione di solito da qualche parte downfield e una grandezza. A volte dobbiamo gestire due vettori insieme lavorando su qualche oggetto. In questi casi gli angoli tra questi vettori sono importanti., Questo argomento spiegherà l’angolo tra due vettori formula così come esempi. Impariamola!
Concetto di vettori
Fuori dal campo, i vettori possono essere utilizzati per rappresentare qualsiasi numero di oggetti o attività fisiche. Biru. Il vento, ad esempio, è una quantità vettoriale. È perché in un dato luogo ha una direzione così come la grandezza. Possiamo fare una mappa del flusso d’aria in qualsiasi momento, quindi, disegnando i vettori del vento per un numero di diverse posizioni geografiche.
Molte proprietà degli oggetti in movimento sono anche tipi di vettori., In billiard ball, il suo vettore di velocità descrive il suo movimento. Esso mostra la direzione dei segni freccia vettore come la direzione del movimento, e la lunghezza del vettore rappresenta la velocità della palla.
Il momento della palla da biliardo è anche un esempio di quantità vettoriale. Poiché è uguale alla massa per velocità. Pertanto, il vettore di quantità di moto dei punti a sfera nella stessa direzione del suo vettore di velocità. E la grandezza del vettore del momento sarà il prodotto di moltiplicazione della velocità della palla e della sua massa.,
In termini di matematica, un vettore è qualsiasi oggetto che ha una grandezza e una direzione definibili. Poiché i vettori non sono gli stessi delle linee o delle forme standard, dobbiamo usare alcune formule speciali per trovare angoli tra di loro.
La formula per l’angolo tra due vettori
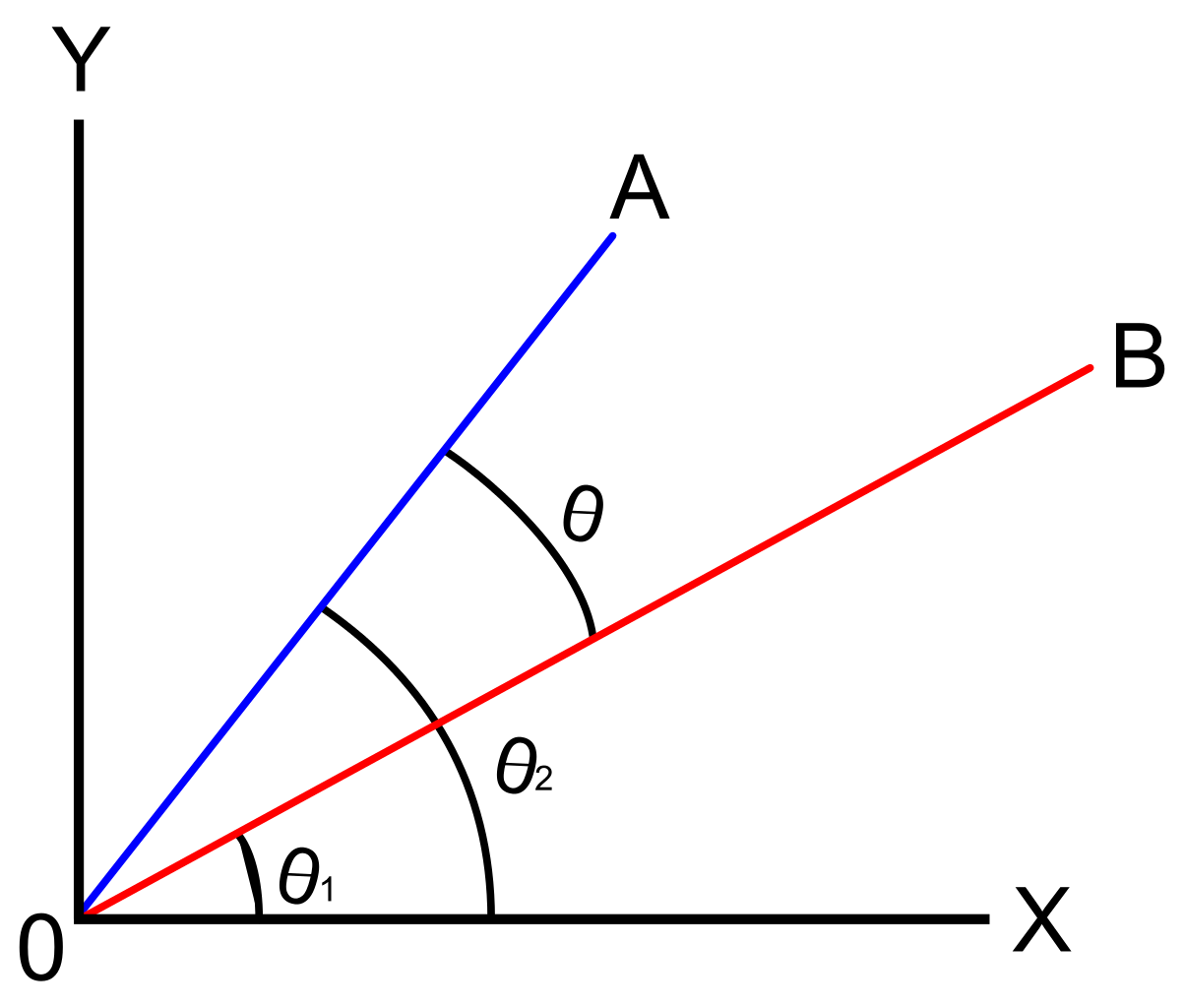
L’angolo tra due vettori sarà differito di un singolo punto, che è chiamato come l’angolo più breve al quale dobbiamo girare intorno a uno dei vettori nella posizione di co-direzionale con un altro vettore.,
La discussione sugli angoli di direzione dei vettori si concentra sulla ricerca dell’angolo di un vettore rispetto all’asse x positivo. Questo si concentrerà sull’angolo tra due vettori nella posizione standard. Si dice che un vettore sia in posizione standard se il suo punto iniziale è l’origine (0, 0).
Se i due vettori sono assunti come a e b, il punto creato viene definito come a .b. Supponiamo che questi due vettori siano separati dall’angolo \ (\theta\). Per sapere qual è la misura dell’angolo risolveremo con l’aiuto della formula data:
Conosciamo il prodotto dot:
\(\vec{a}.,\vec{b} =|\vec{a}||\vec{b}|cos\theta\)
Ora, l’angolo tra due vettori formula è:
\(\theta = cos^{-1}\frac{\vec{a}.\vec{b}} {|\vec{a}||\vec{b}|}\)
Dove \\(theta\) è l’angolo tra i vettori a e b.
Esempi risolti per l’angolo tra due vettori Formula
Q. 1: Calcola l’angolo tra due vettori 3i + 4j-k e 2i – j + k.
Soluzione: Let,
a = 3i + 4j – k e
b = 2i-j + k
Definiamo il prodotto dot come:
a .b = (3i + 4j-k).(2i-j + k)
















Lascia un commento