Radici di un polinomio

Una radice o zero di una funzione è un numero che, quando collegato alla variabile, rende la funzione uguale a zero. Quindi, le radici di un polinomio P(x) sono valori di x tali che P (x) = 0.

Il Teorema degli zeri Razionali

Il Teorema degli Zeri Razionali afferma:

Possiamo usare il Teorema degli Zeri Razionali per trovare tutti gli zeri razionali di un polinomio., Ecco i passaggi:

  1. Disporre il polinomio in ordine decrescente
  2. Annotare tutti i fattori del termine costante. Questi sono tutti i possibili valori di p.
  3. Annota tutti i fattori del coefficiente principale. Questi sono tutti i possibili valori di q.
  4. Annota tutti i possibili valori di . Ricorda che poiché i fattori possono essere negativi, e – devono essere entrambi inclusi. Semplificare ogni valore e cancellare eventuali duplicati.,
  5. Usa la divisione sintetica per determinare i valori di per cui P () = 0. Queste sono tutte le radici razionali di P (x).

Esempio: Trova tutti gli zeri razionali di P(x) = x3-9x + 9 + 2×4-19×2.

Figura %: Divisione sintetica

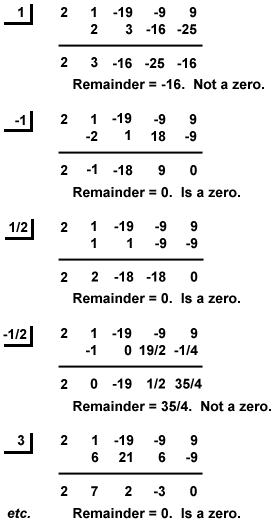
Così, le radici razionali di P(x) sono x = – 3, -1, 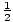, e 3.

Possiamo spesso usare il teorema degli zeri razionali per calcolare un polinomio., Usando la divisione sintetica, possiamo trovare una radice reale a e possiamo trovare il quoziente quando P(x) è diviso per x – a. Successivamente, possiamo usare la divisione sintetica per trovare un fattore del quoziente. Possiamo continuare questo processo fino a quando il polinomio è stato completamente preso in considerazione.