valószínűsége gördülő két kocka a hat oldalú dotssuch mint 1, 2, 3, 4, 5 és 6 pont minden egyes kocka.

ha két kockát egyszerre dobnak, így az események száma 62 = 36 lehet, mivel minden egyes szerszámnak 1-6 száma van az arcán. Ezután a lehetséges eredményeket az alábbi táblázat mutatja.,
Valószínűség – Minta tér két kocka (eredmények):
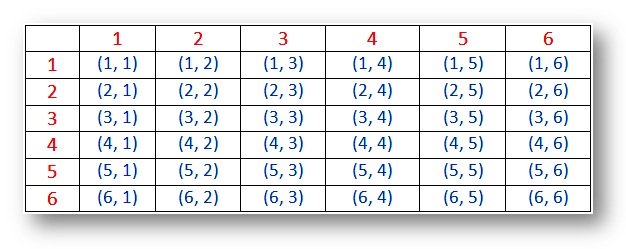
Megjegyzés:
(i) Az eredmények (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) valamint (6, 6) nevezik dublettje.
(ii) a pár (1, 2) és (2, 1) különböző kimenetelek.
kidolgozott problémák járó valószínűség gördülő két kocka:
1. Két kockát dobnak. Legyen az A, B, C a 2, a 3, illetve a 4 összege., Ezután mutassuk meg, hogy
(i) a egy egyszerű esemény
(ii) B és C összetett események
(iii) A és B kölcsönösen kizárják
megoldás:
egyértelműen
A = {(1, 1)}, B = {(1, 2), (2, 1)} és C = {(1, 3), (3, 1), (2, 2)}.
(i) mivel a egyetlen mintapontból áll, ez egy egyszerű esemény.
(ii) mivel mind a B, mind a C több mint egy mintapontot tartalmaz, mindegyik összetett esemény.
(iii) mivel a ∩ B=∅, A és B kölcsönösen kizárják egymást.
2. Két kockát dobnak., A az az esemény, hogy a két kockán feltüntetett számok összege 5, B pedig az az esemény, hogy legalább az egyik kocka 3-at mutat.
a két esemény (i) egymást kölcsönösen kizáró, (ii) kimerítő? Adjon érveket a válasz alátámasztására.
megoldás:
amikor két kocka hengerelt, van n (S) = (6 × 6) = 36.
most, A = {(1, 4), (2, 3), (4, 1), (3, 2)}, és
B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}
(i) A ∩ B = {(2, 3), (3, 2)} ≠ ∅.
ezért az A és B nem zárja ki egymást.,
(ii) is, a ∪ B ≠ S.
ezért az A és B nem kimerítő esemény.
további példák a két kocka dobására vonatkozó valószínűségekkel kapcsolatos kérdésekre.
3. Két kockát dobnak egyszerre.,), hogy egy doublet
(v) egyre összege 8
(vi) egyre összege osztható 5
(vii.) egyre összege legalább 11
(viii.) egyre több a 3-as az összeg
(ix.) egyre összesen legalább 10
(x) egy páros szám, mint a sum
(xi.), hogy egy prímszám, mint a sum
(xii.), hogy egy doublet, a páros számok
(xiii.) egyre több a 2 meghalni, valamint több, a 3, a másik meghal
Megoldás:
Két különböző kockával dobott egyidejűleg, hogy a szám 1, 2, 3, 4, 5, illetve 6 az arcukon., Tudjuk, hogy egy dobott két különböző kocka, az összes lehetséges eredmények száma (6 × 6) = 36.
(i)termékként hatot kap:
Let E1 = termékként hatot kapó esemény. Az a szám, amelynek a terméke hat, E1 = = 4
tehát a “hat mint termék”
a kedvező kimenetelek száma
p(E1) = a lehetséges kimenetelek teljes száma
= 4/36
= 1/9
(ii) az összeg ≤ 3:
Let E2 = az összeg ≤ 3., A szám, amelynek összege ≤ 3 lesz E2 = = 3
ezért, valószínűsége ofgetting “sum ≤ 3′
száma kedvező eredmények
P(E2) = teljes száma lehetséges kimenetele
= 3/36
= 1/12
(iii) getting sum ≤ 10:
Let E3 = event of getting sum ≤ 10. A szám, amelynek összege ≤ 10 lesz E3 =
= 33
ezért valószínűsége, hogy “sum ≤ 10”
száma kedvező eredmények
p(E3) = teljes száma lehetséges kimenetele
= 33/36
= 11/12
(iv)kapok egy doublet:Let E4 = esemény kapok egy doublet., A szám, amely doublet lesz E4 = = 6
ezért valószínűsége, hogy getting “a doublet”
száma kedvező eredmények
P(E4) = teljes száma lehetséges kimenetele
= 6/36
= 1/6
(v)kapok egy összeget 8:
Let E5 = esemény szerzés összege 8. A 8-as számú szám E5 = = 5
lesz, ezért valószínű, hogy “a 8′
a kedvező kimenetelek száma
p(E5) = a lehetséges kimenetelek száma
= 5/36
(vi)az 5-tel osztható összeg megszerzése:
legyen E6 = az 5-tel osztható összeg megszerzése., Az a szám, amelynek összege 5-tel osztható, E6 = = 7
tehát a valószínűsége, hogy ‘sum divisible by 5’
a kedvező kimenetelek száma
p(E6) = a lehetséges kimenetelek száma
= 7/36
(vii) az atleast 11 összege:
Let E7 = az atleast 11 összege. A legalább 11-es összeg eseményei: E7 = = 3
ezért valószínű, hogy ‘legalább 11’
a kedvező kimenetelek száma
p(E7) = a lehetséges kimenetelek teljes száma
= 3/36
= 1/12
(viii) a 3-as amultiple összege:
Let E8 = a 3-as összeg többszörösének összege., A 3-as szorzótényező összege E8 = = 12
, tehát a 3-as szorzótényező valószínűsége ”
a kedvező kimenetelek száma
p(E8) = a lehetséges kimenetelek teljes száma
= 12/36
= 1/3
(ix) összesen legalább 10-et kap:
Let E9 = a legalább 10-et elérő esemény., Az összesen legalább 10 eseménye E9 = = 6
lesz, ezért valószínű, hogy “összesen legalább 10”
a kedvező kimenetelek száma
p(E9) = a lehetséges kimenetelek teljes száma
= 6/36
= 1/6
(x) az egyenérték összege:
legyen E10 = páros szám összege., A páros szám eseményei, mint összeg, E10 = = 18
tehát a páros szám valószínűsége, mint a kedvező kimenetelek összege
p(E10) = a lehetséges kimenetelek teljes száma
= 18/36
= 1/2
(xi) a primenumber összege:
legyen E11 = prímszám összege., Egy prímszám eseményei, mint összeg, E11 = = 15
tehát a prímszám valószínűsége ”
a kedvező kimenetelek száma
p(E11) = a lehetséges kimenetelek teljes száma
= 15/36
= 5/12
(xii) páros számok adoubletje:
Let E12 = páros számok duplázásának eseménye., Az események egy doublet, a páros számok lesz E12 = = 3
Ezért a valószínűsége annak, hogy visszakapom egy doublet, a páros számok’
Számos kedvező eredmények
P(E12) = Összesen több lehetséges kimenetele
= 3/36
= 1/12
(xiii.), hogy amultiple 2 az egyik meghal, valamint több, a 3, a másik meghal:Hadd E13 = esemény, hogy egy több 2 az egyik meghal, valamint több, a 3, a másik meghal., Az egyik halon a 2-es többszöröse, a másikon a 3-as többszöröse E13 = = 11
, ezért valószínű, hogy “az egyik halon a 2-es többszöröse, a másikon a 3-as többszöröse”
a kedvező kimenetelek száma
P(E13) = a lehetséges kimenetelek teljes száma
= 11/36
4. Kettőt dobnak. Keresse meg (i) az esélyeket az 5.összeg megszerzése mellett, és (ii) theodds az összeg megszerzése ellen 6.
megoldás:
tudjuk, hogy egy dobott két die, a teljes számalehetséges kimenetelek (6 × 6) = 36.
legyen s a mintaterület. Ezután n(S) = 36.,
(i)az 5. összeg megszerzése melletti esélyek:
legyen az E1 az 5. összeg megszerzése. Ezután
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒ p(E1) = 4
ezért P(E1) = n (E1) / n (S) = 4/36 = 1/9
⇒ esélye az E1 = P (E1)/ = (1/9)/(1 – 1/9) = 1/8.
(ii) az esélyek az összeg megszerzése ellen 6:
legyen az E2 az összeg megszerzésének eseménye 6. Ezután
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒ p(E2) = 5
ezért p(E2) = n (E2) / n ( S) = 5/36
⇒ esélye E2 = /P (E2) = (1 – 5/36)/(5/36) = 31/5.
5., Két kocka, egy kék és egy narancs, hengerelt egyszerre. Keresse meg annak valószínűségét, hogy
(i) egyenlő számokat kap mindkét
(ii) két szám, amelyek összege 9.,
Megoldás:
A lehetséges eredmények
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
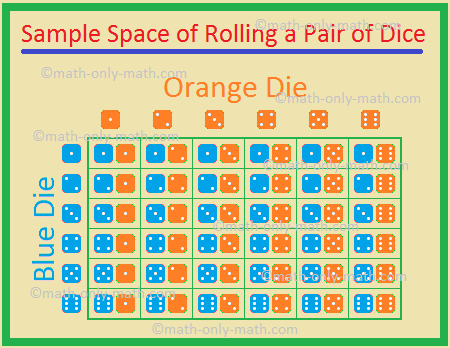
Ezért száma a lehetséges kimenetelek = 36.,
(i) az esemény kedvező kimeneteleinek száma E
= azon eredmények száma, amelyek mindkét kockán egyenlő számmal rendelkeznek
= 6 .
tehát definíció szerint P (E) = \(\frac{6}{36}\)
= \(\frac{1}{6}\)
(ii) az F
esemény kedvező kimeneteleinek száma = azon eredmények száma, amelyekben a rajtuk megjelenő két szám összege 9
= 4 .
így definíció szerint P (F) = \(\frac{4}{36}\)
= \(\frac{1}{9}\).
ezek a példák segítenek a különböző típusú problémák megoldásában a rollingtwo kocka valószínűsége alapján.,p>Probability and Playing Cards
Probability for Rolling Two Dice
Solved Probability Problems
Probability for Rolling Three Dice
9th Grade Math
From Probability for Rolling Two Dice to HOME PAGE
















Vélemény, hozzászólás?