Vektorok széles körben hasznos a tudomány leírni semmit, amelynek mind egy irányba, valamint a nagysága. Általában hegyes nyilak segítségével rajzolják őket, amelyek hossza a vektor nagyságát képviseli. A hátvéd passza egyszerű példa, mert az irány általában valahol lefelé és nagyságban van. Néha meg kell kezelni a két Vektorok együtt dolgozik valamilyen tárgy. Ilyen esetekben a vektorok közötti szögek fontosak., Ez a téma megmagyarázza a két vektor képletének szögét, valamint a példákat. Tanuljuk meg!
fogalma Vektorok
ki a területen, vektorok lehet használni, hogy képviselje tetszőleges számú fizikai tárgyak vagy tevékenységek. Például. A szél például vektoriális mennyiség. Ez azért van, mert bármely adott helyen van egy irányba, valamint a nagysága. A légáramlás térképét bármikor elkészíthetjük, majd a szélvektorokat számos különböző földrajzi helyre rajzolva.
a mozgó objektumok számos tulajdonsága szintén egyfajta vektor., A biliárdgolyóban a sebességvektor leírja mozgását. Ez mutatja A vektor nyíl irányát, mint a mozgás irányát,a vektor hossza pedig a labda sebességét.
a biliárdgolyó lendülete szintén példa a vektoriális mennyiségre. Mivel ez egyenlő a tömeg alkalommal sebesség. Ezért a golyópontok momentumvektora ugyanabban az irányban, mint a sebességvektor. A momentumvektor nagysága pedig a labda sebességének és tömegének szorzata lesz.,
a matematika szempontjából a vektor minden olyan objektum, amelynek meghatározható nagysága és iránya van. Mivel a vektorok nem azonosak a szabványos vonalakkal vagy alakzatokkal, speciális képleteket kell használnunk, hogy szögeket találjunk közöttük.
A két vektor közötti szög képlete
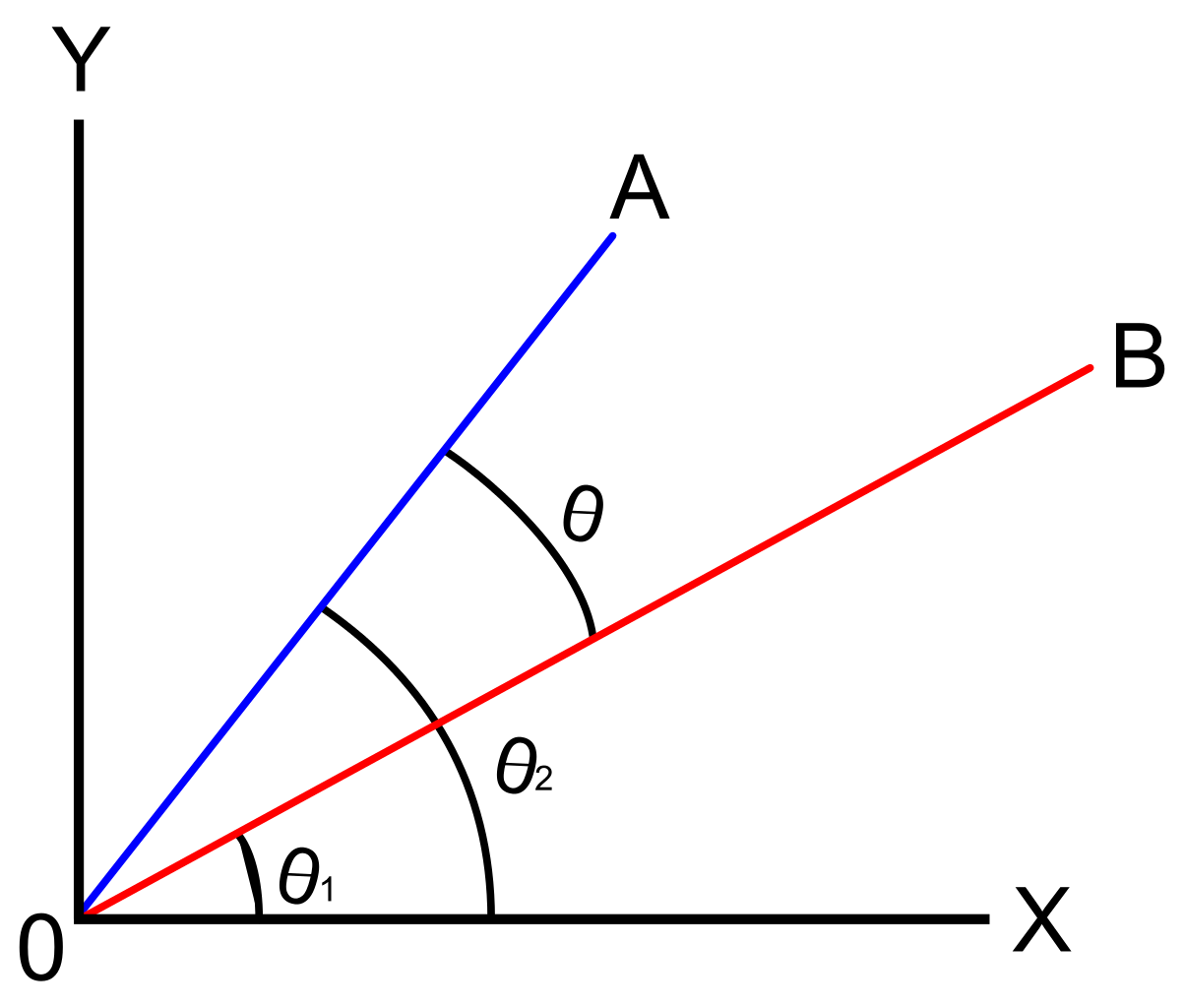
a két vektor közötti szöget egyetlen ponttal halasztják el, amelyet a legrövidebb szögnek neveznek, amelyen az egyik vektor körül kell fordulnunk egy másik vektorral.,
a vektorok irányszögeiről szóló vita arra összpontosít, hogy megtaláljuk a vektor szögét a pozitív x-tengelyhez képest. Ez a két vektor közötti szögre összpontosít a standard helyzetben. Azt mondják, hogy egy vektor normál helyzetben van, ha a kiindulási pontja az eredet (0, 0).
Ha a két vektor ” a ” és “b”, akkor a létrehozott pont “a”.b. tegyük fel, hogy ezt a két vektort szög \(\theta\) választja el. Ahhoz, hogy tudjuk, mi a szögmérés, a megadott képlet segítségével oldjuk meg:
ismerjük a pontterméket:
\(\vec{a}.,\ vec{B} = |\vec{a}||\vec{B}/cos\theta\)
most a két vektor közötti szög:
\(\theta = cos^{-1} \ FRAC{\vec {a}.\ vec{B}} {/\vec{a} / / \ vec{b}/}\)
ahol \ \ (theta\) az A és b Vektorok közötti szög.
Megoldott Példa a Szög Két Vektor Formula
1.: Kiszámolja a szög két vektor 3i + 4j – k 2i – j + k.
Megoldás: Hadd,
a = 3i + 4j – k
b = 2i – j + k
Mi határozza meg a dot termék:
a .b = (3i + 4J – k).(2i – j + k)
















Vélemény, hozzászólás?